Trigonométrie 3AC – Cours

I- Les rapports trigonométriques d’un angle aigu

1) Vocabulaire

$A B C$ est un triangle rectangle en $A$

On considère l’angle $\widehat{A B C}$

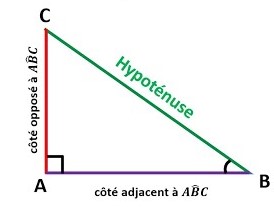
Remarque

✭ De même pour l’angle $\widehat{ACB}$ , le côté adjacent est $AC$ et le côté opposé est $AB$.

✭ Les deux angles $\widehat{ABC}$  et $\widehat{ACB}$  sont aigus, c’est à dire : $0°<\widehat{ABC}< 90°$  et $0° <\widehat{ACB}< 90°$

✭ L’hypoténuse est le plus grand côté parmi les côtés d’un triangle rectangle.

2) Définition

Définition

Dans un triangle $A B C$ rectangle en $A$, les rapports trigonométriques de l’angle $\widehat{A B C}$ sont :

✭ Le rapport $\frac{A B}{B C}$ s’appelle le cosinus de l’angle $\widehat{A B C}$ symbolisé par $\cos \widehat{A B C}$

$\cos \widehat{A B C}=\frac{\text { Côté adjacent à l’angle } \widehat{A B C}}{\text { hypothénuse }}=\frac{A B}{B C}$

✭ Le rapport $\frac{A C}{B C}$ s’appelle le sinus de l’angle $\widehat{A B C}$ symbolisé par $\sin \widehat{A B C}$

$\sin \widehat{A B C}=\frac{\text { Côté opposé à l’angle } \widehat{A B C}}{\text { hypothénuse }}=\frac{A C}{B C}$

✭ Le rapport $\frac{A C}{A B}$ s’appelle la tangente de l’angle $\widehat{A B C}$ symbolisé par $\tan \widehat{A B C}$

$\tan \widehat{A B C}=\frac{\text { Côté opposé à l’angle } \widehat{A B C}}{\text { Côté adjacent à l’angle } \widehat{A B C}}=\frac{A C}{A B}$

 Exemple

Soit $A B C$ un triangle rectangle en $A$ tel que : $A B=3 \mathrm{~cm}, A C=4 \mathrm{~cm}$ et $B C=5 \mathrm{~cm}$

✭ Calculer les rapports trigonométriques de l’angle $\widehat{A B C}$ et de l’angle $\widehat{A C B}$

Solution

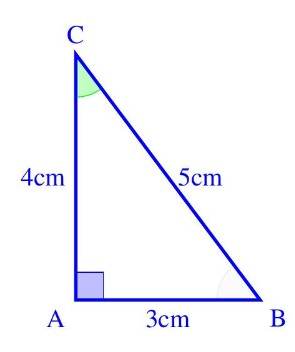
✭ Calcul des rapports trigonométriques de l’angle $\widehat{A B C}$

– $\cos \widehat{A B C}=\frac{A B}{B C}=\frac{3}{5}=0.6$

– $\sin \widehat{A B C}=\frac{A C}{B C}=\frac{4}{5}=0.8$

– $\tan \widehat{A B C}=\frac{A C}{A B}=\frac{4}{3}$

✭ Calcul des rapports trigonométriques de l’angle $\widehat{A C B}$

– $\cos \widehat{A B C}=\frac{A C}{B C}=\frac{4}{5}=0.8$

– $\sin \widehat{A C B}=\frac{A B}{B C}=\frac{3}{5}=0.6$

– $\tan \widehat{A C B}=\frac{A B}{A C}=\frac{3}{4}=0.75$

3) L’emploi de la calculatrice dans le calcul trigonométrique

(1) En employant la calculatrice, calculer les valeurs approchés des rapports trigonométriques de l’angle $\alpha=30^{\circ}$

On a :
$\Rightarrow \cos 30^{\circ}=0.86$
$\Rightarrow \sin 30^{\circ}=\frac{1}{2}=0.5$
$\Rightarrow \tan 30^{\circ}=0.57$

(2) En employant la calculatrice, trouver la valeur de l’angle $\alpha$ dont les rapports trigonométriques sont respectivement : $\cos \alpha_{1}=0.5 \quad , \quad \sin \alpha_{2}=\frac{1}{2}=\frac{\sqrt{2}}{2} \quad et \quad \tan \alpha_{3}=1 $ 

En touchant les boutons Shift $+(\overline{\operatorname{Cos}} \quad \mathrm{ou}  \quad \overline{\operatorname{Sin}} \quad \mathrm{ou}  \quad \overline{\text { Tan }})$ on trouve :

$\Rightarrow \alpha_{1}=60^{\circ}$
$\Rightarrow \alpha_{2}=45^{\circ}$
$\Rightarrow \alpha_{3}=45^{\circ}$

II. Relation entre les rapports trigonométriques d’un angle aigu

1) Proposition : relation entre $\cos$ et $\sin$  d’un angle aigu

Proposition

Soit $\alpha$ la mesure d’un angle aigu $0^{\circ}<\alpha<90^{\circ}$

On a $0<\cos \alpha<1$ et $0<\sin \alpha<1$

Et $\cos ^{2} \alpha+\sin ^{2} \alpha=1$

Remarque

✭ $\cos ^{2} \alpha+\sin ^{2} \alpha=1 \Rightarrow\left\{\begin{array}{l}\cos ^{2} \alpha=1-\sin ^{2} \alpha \\ \sin ^{2} \alpha=1-\cos ^{2} \alpha\end{array}\right.$

✭ C’est à dire, si on sait cos (sin), on peut calculer le sin ( $\cos$ )

✭ On écrit $\cos ^{2} x$ ou $(\cos x)^{2}$ et pas $\cos x^{2}$ (de même pour $\sin$ )

 Exemple

Soit $\alpha$ la mesure d’un angle aigu tel que $\cos \alpha=\frac{2}{3}$
calculer $\sin \alpha$

Solution

Calculons $\sin \alpha$

On sait que : $\cos ^{2} \alpha+\sin ^{2} \alpha=1$, donc $\left(\frac{2}{3}\right)^{2}+\sin ^{2} \alpha=1$, donc $\frac{4}{9}+\sin ^{2} \alpha=1$

Donc $\sin ^{2} \alpha=1-\frac{4}{9}$, donc $\sin ^{2} \alpha=\frac{5}{9}$, donc $\sin \alpha=\sqrt{\frac{5}{9}}$

Alors $\sin \alpha=\frac{\sqrt{5}}{3}$

2) Proposition : relation entre $\cos$ et $\sin$ et $tan$  d’un angle aigu

Proposition

Soit $\alpha$ la mesure d’un angle aigu $0^{\circ}<\alpha<90^{\circ}$

On a : $\tan \alpha=\frac{\cos \alpha}{\sin \alpha}$

Remarque

✭ $\tan \alpha=\frac{\cos \alpha}{\sin \alpha} \Rightarrow\left\{\begin{array}{l}\sin \alpha=\tan \alpha \times \cos \alpha \\ \cos \alpha=\frac{\sin \alpha}{\tan \alpha}\end{array}\right.$

✭ $\alpha$ la mesure d’un angle aigu, on a $\tan \alpha>0$

 Exemple

$1)$ Soit $x$ la mesure d’un angle aigu tel que $\tan x=2 \sqrt{2}$

• Calculer $\cos x$ et $\sin x$

$2)$ Soit $x$ la mesure d’un angle aigu tel que $\sin x=\frac{\sqrt{5}}{3}$

• Calculer $\tan x$

Solution

$1)$ Calculons $\cos x$ et $\sin x$

On a $\tan x=\frac{\sin x}{\cos x}$, donc $2 \sqrt{2}=\frac{\sin x}{\cos x}$, c’est à dire $\sin x=2 \sqrt{2} \cos x$

Or $\sin ^{2}+\cos ^{2} x=1$, donc $(2 \sqrt{2} \cos x)^{2}+\cos ^{2} x=1$

Donc $8 \cos ^{2} x+\cos ^{2} x=1$, donc $9 \cos ^{2} x=1$, donc $\cos ^{2} x=\frac{1}{9}$

D’où $\cos x=\sqrt{\frac{1}{9}}($ car $\cos x>0)$ donc $\cos x=\frac{1}{3}$

Or $\sin x=2 \sqrt{2} \cos x$ donc $\sin x=2 \sqrt{2} \times \frac{1}{3}$

Alors $\sin x=\frac{2 \sqrt{2}}{3}$

$2)$ Calculons $\tan x$

Calculons d’abord $\cos x$

On a $\cos ^{2} x+\sin ^{2} x=1$, donc $\cos ^{2} x+\left(\frac{\sqrt{5}}{3}\right)^{2}=1$, donc $\cos ^{2} x+\frac{5}{9}=1$

Donc $\cos ^{2} x=1-\frac{5}{9}$, donc $\cos ^{2} x=\frac{4}{9}$

D’où $\cos x=\sqrt{\frac{4}{9}}(\operatorname{car} \cos x>0)$

Alors $\cos x=\frac{2}{3}$

On a $\tan x=\frac{\sin x}{\cos x}=\frac{\frac{\sqrt{5}}{3}}{\frac{2}{3}}=\frac{\sqrt{5}}{3} \times \frac{3}{2}=\frac{3 \sqrt{5}}{6}$

Alors $\tan x=\frac{\sqrt{5}}{2}$

3) Proposition : les rapports trigonométriques de deux angles complémentaires

Proposition

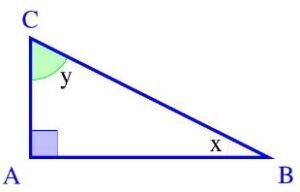
Soit $x$ et $y$ les mesures de deux angles complémentaires, c’est à dire $x+y=90^{\circ}$ Alors :

$ \cos x=\sin y $

$ \sin x=\cos y $

$ \tan x=\frac{1}{\tan y}$

 Exemple

$ \sin 70^{\circ}=\cos 20^{\circ}$

$  \cos 30^{\circ}=\sin 60^{\circ} $

$ \text { tan } 15^{\circ}=\frac{1}{\tan 75^{\circ}} $

$\sin 80^{\circ}=\cos 10^{\circ}$

$ \cos 45^{\circ}=\sin 45^{\circ}$

$ \text { tan } 11^{\circ}=\frac{1}{\tan 79^{\circ}}$

4) Angles particuliers

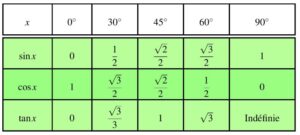
Exemple

Simplifier : $F=\sqrt{2} \cos 45^{\circ}+\sin ^{2} 30^{\circ}+\sin ^{2} 60^{\circ}+\sqrt{3} \tan 30^{\circ}$

Solution

Simplifions $F=\sqrt{2} \cos 45^{\circ}+\sin ^{2} 30^{\circ}+\sin ^{2} 60^{\circ}+\sqrt{3} \tan 30^{\circ}$

 $F=\sqrt{2} \cos 45^{\circ}+\sin ^{2} 30^{\circ}+\sin ^{2} 60^{\circ}+\sqrt{3} \tan 30^{\circ}$

$ =\sqrt{2} \times \frac{\sqrt{2}}{2}+\left(\frac{1}{2}\right)^{2}+\left(\frac{\sqrt{3}}{2}\right)^{2}+\sqrt{3} \times \frac{\sqrt{3}}{3} $

$ =\frac{2}{2}+\frac{1}{4}+\frac{3}{4}+\frac{3}{3}=1+\frac{4}{4}+1 $

$ =1+1+1=3$