Trigonométrie exercices corrigés 3AC
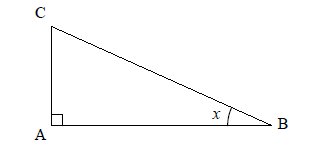
Exercice 1:
$ABC$ est un triangle rectangle en $A$.
$1)$ On considère l’angle aigu $x$ :
$a)$ Quel est le côté opposé à $x$ ?
$b)$ Quel est le côté adjacent à $x$ ?
$c)$ Quelle est l’hypoténuse ?
$2)$ Écrire une formule faisant intervenir
$a)$l’angle $x$, $AB$ et $AC$ :
$b)$ l’angle $x$, $AB$ et $BC$ :
$c)$ l’angle $x$, $AC$ et $BC$ :
$3)$ On considère maintenant l’angle aigu $y$ :
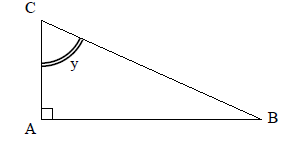
$a)$ Quel est le côté opposé à $y$ ?
$b)$ Quel est le côté adjacent à $y$ ?
$c)$ Quelle est l’hypoténuse ?
$4)$ Écrire une formule faisant intervenir
$a)$ l’angle $y$, $AB$ et $AC$ :
$b)$ l’angle $y$, $AB$ et $BC$ :
$c)$ l’angle $y$, $AC$ et $BC$ :
$ABC$ est un triangle rectangle en $A$.
$1)$ On considère l’angle aigu $x$ :
$a)$ Quel est le côté opposé à $x$ ? $[AC]$
$b)$ Quel est le côté adjacent à $x$ ? $[AB]$
$c)$ Quelle est l’hypoténuse ? $[BC]$
$2)$ Écrire une formule faisant intervenir
$a)$l’angle $x$, $AB$ et $AC$ :
$\tan x=\frac{AC}{AB}$
$b)$ l’angle $x$, $AB$ et $BC$ :
$\cos x=\frac{\mathrm{AB}}{\mathrm{BC}}$
$c)$ l’angle $x$, $AC$ et $BC$ :
$\sin x=\frac{A C}{B C}$
$3)$ On considère maintenant l’angle aigu $y$ :
$a)$ Quel est le côté opposé à $y$ ? $[AB]$
$b)$ Quel est le côté adjacent à $y$ ? $[AC]$
$c)$ Quelle est l’hypoténuse ? $[BC]$
$4)$ Écrire une formule faisant intervenir
$a)$ l’angle $y$, $AB$ et $AC$ :
$\tan y=\frac{A B}{A C}$
$b)$ l’angle $y$, $AB$ et $BC$ :
$\sin y=\frac{A B}{B C}$
$c)$ l’angle $y$, $AC$ et $BC$ :
$\cos y=\frac{A C}{B C}$
Exercice 2:
$ABC$ est un triangle tel que : $AB=12$ ;$AC=5$ et $BC=13$
$1)$ Démontrer que le triangle $ABC$ est rectangle en $A$
$2)$ Calculer : $\cos \hat{B} ; \sin \hat{B}$ et $\tan \hat{B}$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 3:
Le triangle $ABC$ est rectangle en $A$ tel que $AB = \sqrt{3}$ et $\tan \hat{B}= \sqrt{2}$
$1)$ Prouver que $AC =\sqrt{6}$
$2)$ Déduire : $BC$
$3)$ Calculer : $\cos \hat{B} ; \sin \hat{B}$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 4:
$1)$ À l’aide de la calculatrice, donne la valeur approchée de:
$\cos 18° ; \sin 42°$ ; $\tan 88°$
$2)$ Dans chaque cas, donne la valeur arrondie au degré de $x$.
$\cos x=0,23 ; \sin x=0,32$ ; $\tan x=36$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 5:
ABC est un triangle rectangle en $C$. On connaît $BC = 4cm$ et $ \hat{A}= 45°$
$1)$ Ecrire les expressions de $\cos \hat{A} ; \sin \hat{A}$ et $\tan \hat{A}$ en fonction des côtés.
$2)$ Quelle expression permet de calculer $AB$ ?
$3)$ Calculer $AB$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 6:
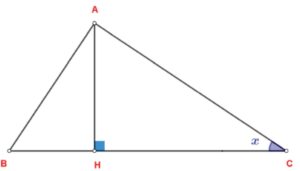
Soit $H$ le pied de la hauteur issue de $B$. On a : $BC=6,5$, $AH=2$ et $HC=5,2$
$1)$ Calculer $BH$
$2)$ Calculer $ \sin H \widehat{B} C$ ,En déduire la mesure de l’angle $H \widehat{B} C$ .
$3)$ Calculer la mesure de l’angle $A \widehat{B} H$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 7:
$1)$ Calculer $\sin x$ et $\tan x$ sachant que : $ \cos x = 0,8$
$2)$ Calculer $\cos x$, et $\tan x$ sachant que : $\sin x =\frac{1}{3} $
$3)$ Calculer $\sin x$ et $\tan x$ sachant que : $\cos x = 0,6$
$4)$ Calculer $\cos x$, et $\tan x$ sachant que : $\sin x =\frac{2}{\sqrt{6}}$
$5)$ Calculer $\cos x$ et $\sin x$ sachant que : $\tan x =\frac{1}{3} $
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 8:
1) Simplifier et calculer :
$ A=\cos ^{2} 35^{\circ}+\sin ^{2} 33^{\circ}+\sin ^{2} 35^{\circ}+\cos ^{2} 33^{\circ} $
$ B=\cos ^{2} 20^{\circ}+\sin ^{2} 20+1 $
$ C=\cos ^{2} 25^{\circ}+\sin ^{2} 70^{\circ}+\sin ^{2} 25^{\circ}+\cos ^{2} 70^{\circ} $
2) Simplifier et calculer :
$A=\cos ^{2} x+3 \sin ^{2} x-2$
$B=(\cos x+\sin x)^{2}+(\cos x-\sin x)^{2}$
$C=\frac{\sin ^{4} x-\cos ^{4} x}{\sin x+\cos x}$
$D=\sqrt{1+\cos x} \times \sqrt{1-\cos x} \times \frac{1}{\sin x}$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 9:
$1)$ Montrer que:
• $\frac{1}{\cos ^{2} x}=1+\tan ^{2} x$
• $ \frac{1}{\sin ^{2} x}=1+\frac{1}{\tan ^{2} x} $
• $ \frac{(1+\cos \alpha)(1-\cos \alpha)}{2 \sin ^{2} \alpha}=\frac{1}{2} $
$2)$ Simplifier les expressions suivantes :
• $\frac{1}{\cos ^{2} \alpha}-\left(1-\tan ^{2} \alpha\right)$
• $(1-\sin \alpha)(1+\sin \alpha)\left(1+\tan ^{2} \alpha\right)+2012$
• $\sin ^{4} x+\cos ^{4} x+2 \sin ^{2} x \times \cos ^{2} x$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 10:
$x$ est la mesure d’un angle aigu. Déterminer la valeur de $x$ dans chaque cas :
$1)$ $\sin x = \cos 45°$
$2)$ $\cos x = \sin 15°$
$3)$ $\sin x = \cos 70°$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 11:
$ A=\cos ^{2} 10^{\circ}+\sin ^{2} 40^{\circ}+\cos ^{2} 80^{\circ}+\sin ^{2} 50^{\circ} $
$ B=\cos 25^{\circ}+\cos 70^{\circ}-\sin 65^{\circ}+\sin 20^{\circ} $
$ C=\cos ^{2} 15^{\circ}+\cos ^{2} 75^{\circ}-2 \tan 35^{\circ} \times \tan 55^{\circ} $
$ D=\sin 25^{\circ}-\sin 65^{\circ}+\cos 25^{\circ}-\cos 65^{\circ} $
$ E=\sin 80^{\circ}+7 \sin ^{2} 50^{\circ}-\cos 10^{\circ}+7 \sin ^{2} 40^{\circ} $
$ F=3 \cos ^{2} 15+3 \cos ^{2} 75^{\circ}-2 \times \tan 35^{\circ} \times \tan 55^{\circ} $
$ G=2 \sin ^{2} 25^{\circ}+\sin 13^{\circ}+2 \cos ^{2} 65^{\circ}-\cos 77^{\circ}$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 12:
$A=\sin 55^{\circ}-\cos 35^{\circ}+\cos 70^{\circ}-\sin 20^{\circ}$
$B=\sin ^{2} 29^{\circ}-\tan 75^{\circ} \times \tan 15^{\circ}+\sin ^{2} 61^{\circ}$
$C=\sin 23^{\circ} \times \cos 67^{\circ}+\sin ^{2} 67^{\circ}+\tan 40^{\circ} \times \tan 50^{\circ}$
$D=2 \cos ^{2} 24^{\circ}-\sin ^{2} 68^{\circ}+2 \cos ^{2} 66^{\circ}+\cos ^{2} 22^{\circ}$
$E=\cos ^{2} 35^{\circ}-\tan 45^{\circ}+\cos ^{2} 55^{\circ}+\sin ^{2} 30^{\circ}$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 13:
$I)$ $b$ est la mesure d’un angle aigu tel que : $2 \cos (b)=\sin (b)$
$1)$ Calculer : $\boldsymbol{\operatorname { t a n }}(b), \sin (b)$ et $\boldsymbol{\operatorname { c o s }}(b)$.
$2)$ Calculer: $M=1+\frac{3}{\sqrt{3}} \sin \left(35^{\circ}\right)-\sqrt{3} \cos \left(55^{\circ}\right) $.
$II)$ $3 \quad A B C$ est un triangle et $H$ est le projeté orthogonal de $A$ sur (BC) tel que : $A H=4, B H=2$ et $\tan (x)=\frac{1}{2}$.
$a)$ Montrer que: $A B=2 \sqrt{5}, A C=4 \sqrt{5}$ et $C H=8$
$b)$ Montrer que le triangle $A B C$ est rectangle en $A$.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Trigonométrie exercices corrigés 3AC