Vecteurs et translation 2AC exercices corrigés
Exercice 1:
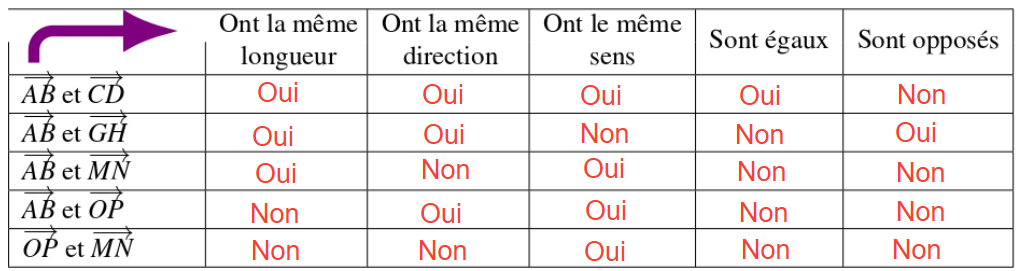
On considère la figure ci-dessous :
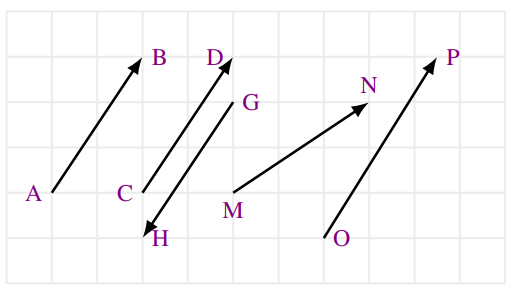
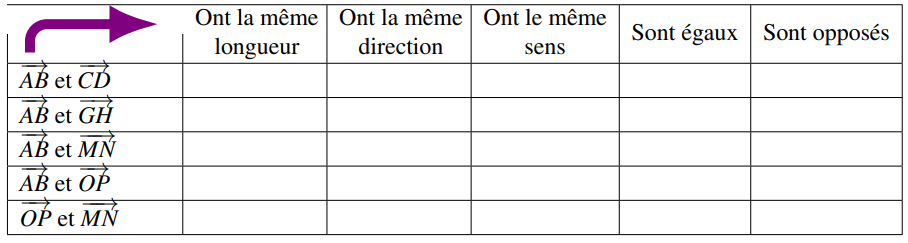
Compléter le tableau suivant par $’Oui’$ ou $’Non’$ :
Exercice 2:
$A$ et $B$ sont deux points distincts.
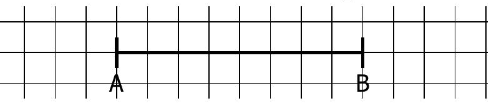
$a)$ Placer le point $M$ tel que $\overrightarrow{B M}=\frac{1}{2} \overrightarrow{A B}$
$b)$ Compléter les égalités suivantes :
$\overrightarrow{\mathrm{AB}}=\ldots \ldots \cdot \overrightarrow{\mathrm{BM}}$
$\overrightarrow{\mathrm{BM}}=\ldots . . \overrightarrow{\mathrm{AM}}$
$\overrightarrow{\mathrm{AM}}=\ldots . . \overrightarrow{\mathrm{AB}}$
$\overrightarrow{\mathrm{MB}}=\ldots . \overrightarrow{\mathrm{AB}}$
$\overrightarrow{\mathrm{BA}}=\ldots . . \overrightarrow{\mathrm{BM}}$
$\overrightarrow{\mathrm{AM}}=\ldots . . \overrightarrow{\mathrm{BM}}$
$a)$

$b)$
$\overrightarrow{\mathrm{AB}}=2 \overrightarrow{\mathrm{BM}}$
$\overrightarrow{\mathrm{BM}}=\frac{1}{3} \overrightarrow{\mathrm{AM}} $
$\overrightarrow{\mathrm{AM}}=\frac{3}{2} \overrightarrow{\mathrm{AB}} $
$\overrightarrow{\mathrm{MB}}=-\frac{1}{2} \overrightarrow{\mathrm{AB}} $
$\overrightarrow{\mathrm{BA}}=-2 \overrightarrow{\mathrm{BM}} $
$\overrightarrow{\mathrm{AM}}=3 \overrightarrow{\mathrm{BM}}$
Exercice 3:
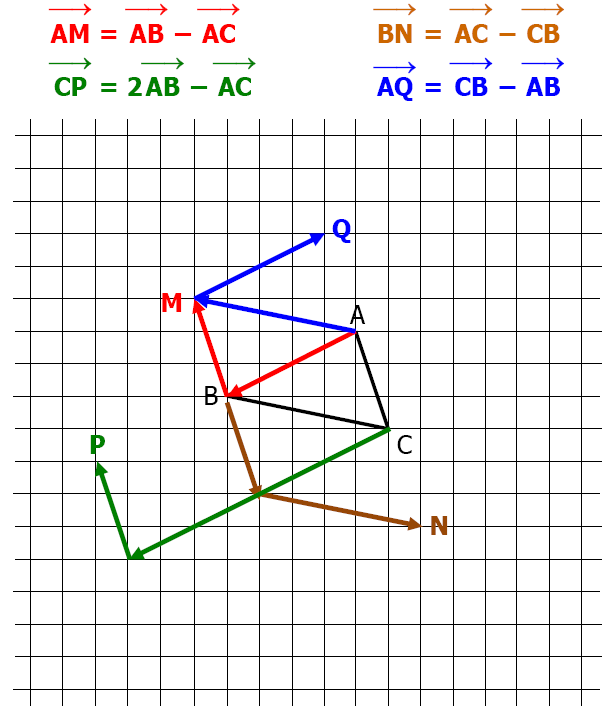
ABC est un triangle.
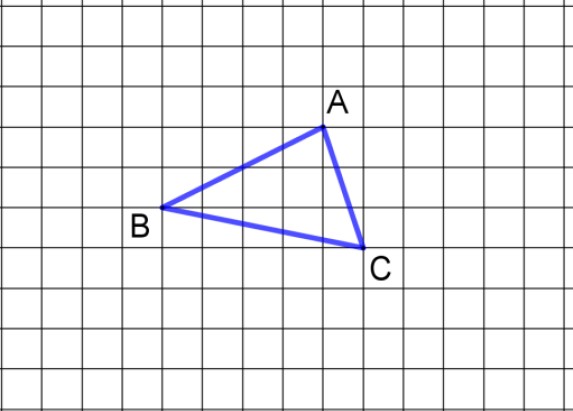
$1)$ Représenter les points $\mathrm{M}, \mathrm{N}, \mathrm{P}$ et Q tels que :
$\overrightarrow{\mathrm{AM}}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}} $
$\overrightarrow{\mathrm{BN}}=\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{BA}} $
$\overrightarrow{\mathrm{CP}}=2 \overrightarrow{\mathrm{AB}} $
$\overrightarrow{\mathrm{AQ}}=\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{AC}}$
$2)$ Représenter les points $\mathrm{M}, \mathrm{N}, \mathrm{P}$ et Q tels que :
$\overrightarrow{\mathrm{AM}}=\overrightarrow{\mathrm{AB}}-\overrightarrow{\mathrm{AC}} $
$\overrightarrow{\mathrm{BN}}=\overrightarrow{\mathrm{AC}}-\overrightarrow{\mathrm{CB}} $
$\overrightarrow{\mathrm{CP}}=2 \overrightarrow{\mathrm{AB}}-\overrightarrow{\mathrm{AC}} $
$\overrightarrow{\mathrm{AQ}}=\overrightarrow{\mathrm{CB}}-\overrightarrow{\mathrm{AB}}$
$1)$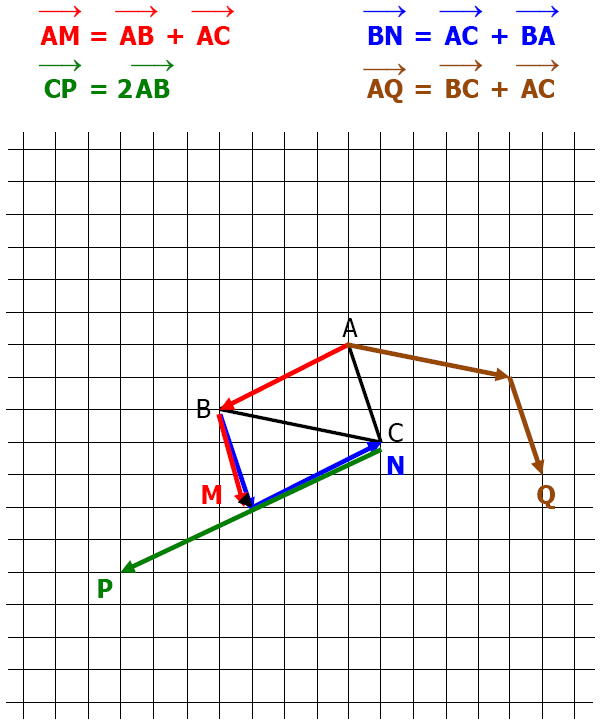
$2)$
Exercice 4:
On donne le triangle ABC suivant :

$a)$ Construire : les points $\mathrm{M}, \mathrm{N}, \mathrm{P}, \mathrm{Q}$ et \mathrm{R} définis par :
$- $Le point $M$ tel que $\overrightarrow{A M}=2 \overrightarrow{B C}$
$-$ Le point $N$ tel que $\overrightarrow{\mathrm{BN}}=\frac{2}{3} \overrightarrow{\mathrm{AC}}$
$-$ Le point $P$ tel que $\overrightarrow{C P}=2 \overrightarrow{A B}-\frac{1}{3} \overrightarrow{A C}$
$-$ Le point $Q$ tel que $\overrightarrow{\mathrm{AQ}}=-\frac{4}{3} \overrightarrow{\mathrm{AC}}$
$-$ Le point $R$ tel que $\overrightarrow{A R}=-\frac{3}{4} \overrightarrow{B C}$
$b)$ Montrer que $\overrightarrow{P N}=\overrightarrow{B A}$
$a)$
$b)$
$\overrightarrow{\mathrm{PN}}=\overrightarrow{\mathrm{PC}}+\overrightarrow{\mathrm{CB}}+\overrightarrow{\mathrm{BN}}$
$ =-2 \overrightarrow{\mathrm{AB}}+\frac{1}{3} \overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{CB}}+\frac{2}{3} \overrightarrow{\mathrm{AC}} $
$=2\overrightarrow{\mathrm{BA}}+\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{CB}} $
$=\overrightarrow{\mathrm{BA}}+\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{CB}}+\overrightarrow{\mathrm{BA}} $
$=\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{CA}}=\overrightarrow{\mathrm{BA}}$
Exercice 5:
A l’aide de la relation de Chasles, écrire sous forme d’un seul vecteur… si c’est possible :
$\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{DF}}=$
$\overrightarrow{C B}-\overrightarrow{C A}=$
$\overrightarrow{\mathrm{DF}}-\overrightarrow{\mathrm{FG}}=$
$\overrightarrow{\mathrm{AB}}-\overrightarrow{\mathrm{AC}}=$
$\overrightarrow{\mathrm{RS}}+\overrightarrow{\mathrm{AR}}=$
$\overrightarrow{\mathrm{EG}}+\overrightarrow{\mathrm{GT}}=$
$\overrightarrow{\mathrm{AL}}-\overrightarrow{\mathrm{LA}}=$
$-\overrightarrow{A D}-\overrightarrow{D B}=$
$\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{DF}}=\overrightarrow{\mathrm{AF}}$
$\overrightarrow{C B}-\overrightarrow{C A}=\overrightarrow{AB}$
$\overrightarrow{\mathrm{DF}}-\overrightarrow{\mathrm{FG}}=\overrightarrow{\mathrm{DF}}+\overrightarrow{\mathrm{GF}}$
$\overrightarrow{\mathrm{AB}}-\overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{CB}}$
$\overrightarrow{\mathrm{RS}}+\overrightarrow{\mathrm{AR}}=\overrightarrow{\mathrm{AS}}$
$\overrightarrow{\mathrm{EG}}+\overrightarrow{\mathrm{GT}}=\overrightarrow{\mathrm{ET}}$
$\overrightarrow{\mathrm{AL}}-\overrightarrow{\mathrm{LA}}=\overrightarrow{\mathrm{AL}}+\overrightarrow{\mathrm{AL}}$
$-\overrightarrow{\mathrm{AD}}-\overrightarrow{\mathrm{DB}}=\overrightarrow{\mathrm{BA}}$
Exercice 6:
$1)$ Ecrire plus simplement les vecteurs suivants, en utilisant la relation de Chasles:
$\vec{u}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{CA}} $
$\vec{v}=\overrightarrow{\mathrm{IJ}}+\overrightarrow{\mathrm{KI}}+\overrightarrow{\mathrm{JK}} $
$\vec{w}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{BC}} $
$\vec{x}=\overrightarrow{\mathrm{DE}}+\overrightarrow{\mathrm{FG}}+\overrightarrow{\mathrm{EF}}+\overrightarrow{\mathrm{DG}}$
$2)$ Ecrire plus simplement les vecteurs suivants, en transformant les soustractions en addition de l’opposé, puis en utilisant la relation de Chasles:
$\vec{u}=\overrightarrow{\mathrm{AB}}-\overrightarrow{\mathrm{AC}}$
$\vec{v}=\overrightarrow{\mathrm{RT}}-\overrightarrow{\mathrm{ST}}+\overrightarrow{\mathrm{RS}}$
$\vec{w}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{MA}}-\overrightarrow{\mathrm{MB}}+\overrightarrow{\mathrm{BA}}$
$\vec{x}=2 \overrightarrow{\mathrm{MN}}-\overrightarrow{\mathrm{MP}}-\overrightarrow{\mathrm{PQ}}+\overrightarrow{\mathrm{MQ}}$
$1)$
$\vec{u}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{CA}}$
$\vec{u}=\overrightarrow{\mathrm{AA}}=\overrightarrow{0}$
$\vec{v}=\overrightarrow{\mathrm{IJ}}+\overrightarrow{\mathrm{KI}}+\overrightarrow{\mathrm{JK}}$
$\vec{v}=\overrightarrow{\mathrm{KI}}+\overrightarrow{\mathrm{IJ}}+\overrightarrow{\mathrm{JK}}$
$\vec{v}=\overrightarrow{\mathrm{KK}}=\overrightarrow{\mathrm{O}}$
$\vec{w}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{BC}}$
$\vec{w}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{AC}}$
$\vec{w}=\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{AC}}=2 \overrightarrow{\mathrm{AC}}$
$\vec{x}=\overrightarrow{\mathrm{DE}}+\overrightarrow{\mathrm{FG}}+\overrightarrow{\mathrm{EF}}+\overrightarrow{\mathrm{DG}}$
$\vec{x}=\overrightarrow{\mathrm{DE}}+\overrightarrow{\mathrm{EF}}+\overrightarrow{\mathrm{FG}}+\overrightarrow{\mathrm{DG}}$
$\vec{x}=\overrightarrow{\mathrm{DG}}+\overrightarrow{\mathrm{DG}}=2 \overrightarrow{\mathrm{DG}}$
$2)$
$\vec{u}=\overrightarrow{\mathrm{AB}}-\overrightarrow{\mathrm{AC}}$
$\vec{u}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{CA}}$
$\vec{u}=\overrightarrow{\mathrm{CB}}$
$\vec{v}=\overrightarrow{\mathrm{RT}}-\overrightarrow{\mathrm{ST}}+\overrightarrow{\mathrm{RS}}$
$\vec{v}=\overrightarrow{\mathrm{RT}}+\overrightarrow{\mathrm{TS}}+\overrightarrow{\mathrm{RS}}$
$\vec{v}=\overrightarrow{\mathrm{RS}}+\overrightarrow{\mathrm{RS}}$
$\vec{v}=2 \overrightarrow{\mathrm{RS}}$
$\vec{w}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{MA}}-\overrightarrow{\mathrm{MB}}+\overrightarrow{\mathrm{BA}}$
$\vec{w}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BA}}+\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{BM}}$
$\vec{w}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BA}}+\overrightarrow{\mathrm{BA}}$
$\vec{w}=\overrightarrow{\mathrm{BA}}$
$\vec{x}=2 \overrightarrow{\mathrm{MN}}-\overrightarrow{\mathrm{MP}}-\overrightarrow{\mathrm{PQ}}+\overrightarrow{\mathrm{MQ}}$
$\vec{x}=2 \overrightarrow{\mathrm{MN}}+\overrightarrow{\mathrm{PM}}+\overrightarrow{\mathrm{QP}}+\overrightarrow{\mathrm{MQ}}$
$\vec{x}=2 \overrightarrow{\mathrm{MN}}+\overrightarrow{\mathrm{PM}}+\overrightarrow{\mathrm{MQ}}+\overrightarrow{\mathrm{QP}}$
$\vec{x}=2 \overrightarrow{\mathrm{MN}}+\overrightarrow{\mathrm{PM}}+\overrightarrow{\mathrm{MP}}$
$\vec{x}=2 \overrightarrow{\mathrm{MN}}$
Exercice 7:
Compléter les égalités vectorielles :
1. $\overrightarrow{A B}=\overrightarrow{A E}+\overrightarrow{\ldots B}$
2. $\overrightarrow{\mathrm{IJ}}=\overrightarrow{\mathrm{IL}}+\overrightarrow{\ldots}$
3. $\overrightarrow{\mathrm{RT}}=\ldots . . \overrightarrow{\mathrm{AT}}$
4. $\overrightarrow{\mathrm{SD}}=\overrightarrow{\mathrm{TD}}+\ldots .$.
5. $\overrightarrow{R E}=\overrightarrow{\ldots . .}+\overrightarrow{R S}$
6. $\overrightarrow{\mathrm{CD}}=\overrightarrow{\mathrm{C} \ldots}+\overrightarrow{\mathrm{KL}}+\overrightarrow{\ldots D}$
7. $\overrightarrow{\mathrm{FA}}=\overrightarrow{\mathrm{C} \ldots}+\overrightarrow{\mathrm{FG}}+\overrightarrow{\mathrm{G} \ldots}$
8. $\overrightarrow{A T}=\overrightarrow{A B}+\overrightarrow{R T}+\overrightarrow{B S}+\ldots \ldots$
9. $\overrightarrow{\mathrm{AB}}=\ldots \ldots+\overrightarrow{\mathrm{JK}}+\ldots \ldots$
1. $\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{AE}}+\overrightarrow{\mathrm{EB}}$
2. $\overrightarrow{\mathrm{IJ}}=\overrightarrow{\mathrm{IL}}+\overrightarrow{\mathrm{LJ}}$
3. $\overrightarrow{\mathrm{RT}}=\overrightarrow{\mathrm{RA}}+\overrightarrow{\mathrm{AT}}$
4. $\overrightarrow{\mathrm{SD}}=\overrightarrow{\mathrm{TD}}+\overrightarrow{\mathrm{ST}}$
5. $\overrightarrow{\mathrm{RE}}=\overrightarrow{\mathrm{SE}}+\overrightarrow{\mathrm{RS}}$
6. $\overrightarrow{\mathrm{CD}}=\overrightarrow{\mathrm{CK}}+\overrightarrow{\mathrm{KL}}+\overrightarrow{\mathrm{LD}}$
7. $\overrightarrow{\mathrm{FA}}=\overrightarrow{\mathrm{CA}}+\overrightarrow{\mathrm{FG}}+\overrightarrow{\mathrm{GC}}$
8.$\overrightarrow{\mathrm{AT}}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{RT}}+\overrightarrow{\mathrm{BS}}+\overrightarrow{\mathrm{SR}}$
9. $\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{AJ}}+\overrightarrow{\mathrm{JK}}+\overrightarrow{\mathrm{KB}}$
Vecteurs et translation 2AC exercices corrigés
Exercice 8:
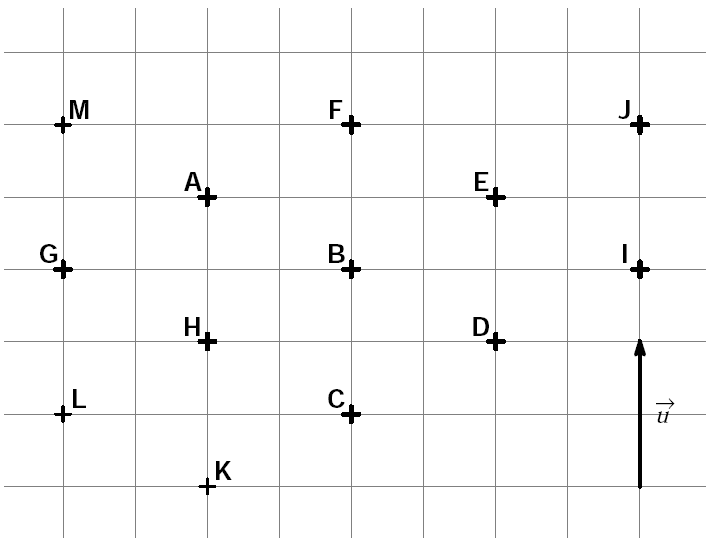
$1) $Quelles sont les images de $A ; C ; H ; D$ et $L$ par la translation de vecteur $\overrightarrow{G A}$ ?
$2)$ Quels sont les vecteurs égaux au vecteur $\vec{u}$ ?
$3)$ Quelles sont les images de $K ; D ; B ; I$ et $G$ parla translation de vecteur $\overrightarrow{H A}$ ?
$4)$ Quel point a pour image $A$ par la translation de vecteur $\overrightarrow{C D}$ ?
$5)$ Quel point a pour image $H$ par la translation de vecteur $\overrightarrow{E A}$ ?
$6)$ Quel point a pour image $J$ par la translation de vecteur $\overrightarrow{L H}$ ?
$7)$ Quelles sont les images de $L$; $H$ et $D$ par la translation de vecteur $\overrightarrow{K B}$ ?
$8)$ Quelles sont les images de $F ; I ; B$ et $E$ par la translation de vecteur $\overrightarrow{J B}$ ?
$9)$ Donner tous les vecteurs égaux au vecteur $\overrightarrow{B I}$.
$10)$ Donner tous les vecteurs égaux au vecteur $\overrightarrow{C A}$.
$1)$ L’image de $A$ par la translation de vecteur $\overrightarrow{G A}$ est $F$.
L’image de $C$ par la translation de vecteur $\overrightarrow{G A}$ est $D$. L’image de $H$ par la translation de vecteur $\overrightarrow{G A}$ est $B$. L’image de $D$ par la translation de vecteur $\overrightarrow{G A}$ est $I$. L’image de $L$ par la translation de vecteur $\overrightarrow{G A}$ est $H$.
$2) $$\vec{u}=\overrightarrow{L G}=\overrightarrow{G M}=\overrightarrow{K H}=\overrightarrow{H A}=\overrightarrow{C B}=\overrightarrow{B F}=$ $\overrightarrow{D E}=\overrightarrow{I J}$
$3)$ L’image de $K$ par la translation de vecteur $\overrightarrow{H A}$ est $H$.
L’image de $D$ par la translation de vecteur $\overrightarrow{H A}$ est $E$.
L’image de $B$ par la translation de vecteur $\overrightarrow{H A}$ est $F$.
L’image de I par la translation de vecteur $\overrightarrow{H A}$ est $J$.
L’image de $G$ par la translation de vecteur $\overrightarrow{H A}$ est $M$.
$4)$ C’est le point $G$ qui a pour image $A$ par la translation de vecteur $\overrightarrow{C D}$.
$5)$ C’est le point $D$ qui a pour image $H$ par la translation de vecteur $\overrightarrow{E A}$.
$6)$ C’est le point $E$ qui a pour image $J$ par la translation de vecteur $\overrightarrow{L H}$.
$7)$ L’image de $L$ par la translation de vecteur $\overrightarrow{K B}$ est $A$.
L’image de $H$ par la translation de vecteur $\overrightarrow{K B}$ est $F$. L’image de $D$ par la translation de vecteur $\overrightarrow{K B}$ est $J$.
$8)$ L’image de $F$ par la translation de vecteur $\overrightarrow{J B}$ est $G$.
L’image de I par la translation de vecteur $\overrightarrow{J B}$ est $C$.
L’image de $B$ par la translation de vecteur $\overrightarrow{J B}$ est $L$.
L’image de $E$ par la translation de vecteur $\overrightarrow{J B}$ est $H$.
$9)$ $\overrightarrow{B I}=\overrightarrow{M F}=\overrightarrow{F J}=\overrightarrow{A E}=\overrightarrow{B G}=\overrightarrow{H D}=\overrightarrow{L C}$
$10)$ $\overrightarrow{C A}=\overrightarrow{H M}=\overrightarrow{K G}=\overrightarrow{D F}$
Exercice 9:
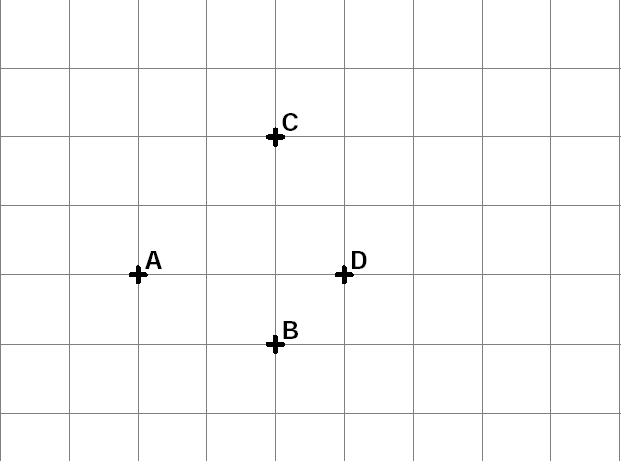
$1)$ Construire $E$ et $F$, images des points $A$ et $B$ par la translation de vecteur $\overrightarrow{D C}$. Ecrire les égalités de vecteurs correspondantes.
$2)$ Construire $G$ et $H$, images des points $D$ et $A$ par la translation de vecteur $\overrightarrow{C A}$. Ecrire les égalités de vecteurs correspondantes.
$3)$ Construire $I$ et $J$, images des points $E$ et $D$ par la translation de vecteur $\overrightarrow{A C}$. Ecrire les égalités de vecteurs correspondantes.
$4)$ Quelle est l’image du point $G$ par la translation de vecteur $\overrightarrow{A D}$ ?
$5)$ Quelle est la nature du quadrilatère $A F B G$ ? Justifier.
$6)$ Quelle est la nature du quadrilatère $CJGH$ ? Justifier.
$7)$ Quelle est la nature du quadrilatère $ECGH$ ? Justifier.
$8)$ Que représente $A$ pour $[E G]$ ? Justifier.
$9)$ Que représente $C$ pour $[DI]$ ? Justifier.
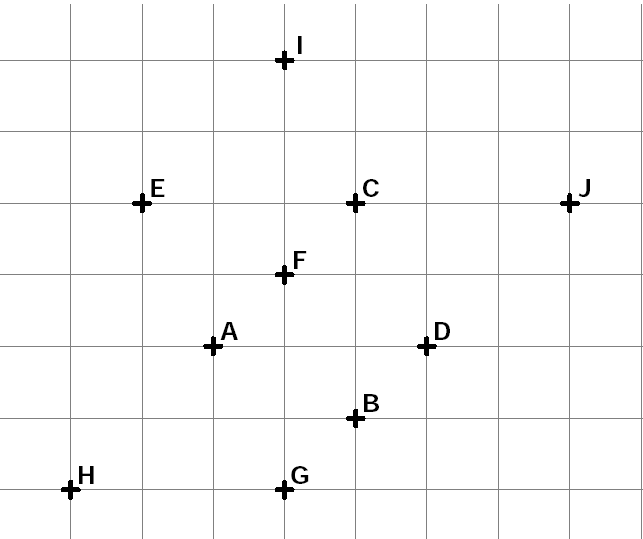
$1)$ $\overrightarrow{D C}=\overrightarrow{A E}=\overrightarrow{B F}$
$2)$ $\overrightarrow{C A}=\overrightarrow{D G}=\overrightarrow{A H}$
$3)$ $\overrightarrow{A C}=\overrightarrow{E I}=\overrightarrow{D J}$
$4)$ L’image du point $G$ par la translation de vecteur $\overrightarrow{A l}$ est $C$.
$5)$ Comme $\overrightarrow{C A}=\overrightarrow{D G}$, alors $A C D G$ est un parallélogramme et on a donc aussi $\overrightarrow{G A}=\overrightarrow{D C}$. Or $\overrightarrow{D C}=\overrightarrow{B F}$ donc $\overrightarrow{G A}=\overrightarrow{B F}$ ce qui signifie que $A F B G$ est un parallélogramme.
$6)$ Comme $\overrightarrow{A C}=\overrightarrow{D J}$, on peut dire que $A C J D$ est un parallélogramme et on a aussi $\overrightarrow{C J}=\overrightarrow{A D}$. Par ailleurs, $\overrightarrow{A H}=\overrightarrow{D G}$ donc $A H G D$ est un parallélogramme et on a aussi $\overrightarrow{A D}=\overrightarrow{H G}$.
On en déduit que $\overrightarrow{C J}=\overrightarrow{H G}$ et donc $C J G H$ est un parallélogramme.
$7)$ On sait que $\overrightarrow{D C}=\overrightarrow{A E}$ donc $A E C D$ est un parallélogramme et on a aussi $\overrightarrow{A D}=\overrightarrow{E C}$. Par ailleurs, dans la question précédente, nous avons montré que $\overrightarrow{A D}=\overrightarrow{H G}$ donc $\overrightarrow{H G}=\overrightarrow{E C}$ ce qui montre que $E C G H$ est un parallélogramme.
$8)$ A la question 5, nous avons montré que $\overrightarrow{G A}=\overrightarrow{D C}$ or $\overrightarrow{D C}=\overrightarrow{A E}$ donc $\overrightarrow{G A}=\overrightarrow{A E}$ ce qui montre que $A$ es le milieu de [GE].
$9)$ On sait que $\overrightarrow{A C}=\overrightarrow{E I}$ donc $A C I E$ est un parallélogramme et donc on a aussi $\overrightarrow{A E}=\overrightarrow{C I}$. De plus, $\overrightarrow{A E}=\overrightarrow{D C}$ donc $\overrightarrow{D C}=\overrightarrow{C I}$ ce qui montre que $C$ est le milieu de $[D I]$.
Exercice 10:
$1)$ Construire un triangle équilatéral ABC de côté 4 cm
$2)$ Construire le point M , image du point B dans la translation de vecteur $\overrightarrow{\mathrm{AC}}$.
$3)$ Quelle est la nature du quadrilatère ABMC ? Justifier.
$4) $-$a)$ Construire le point $N$ tel que $\overrightarrow{C N}=\overrightarrow{C A}+\overrightarrow{C B}$.
$b)$ Montrer que le triangle ANB est équilatéral.
$1)$ et $2)$
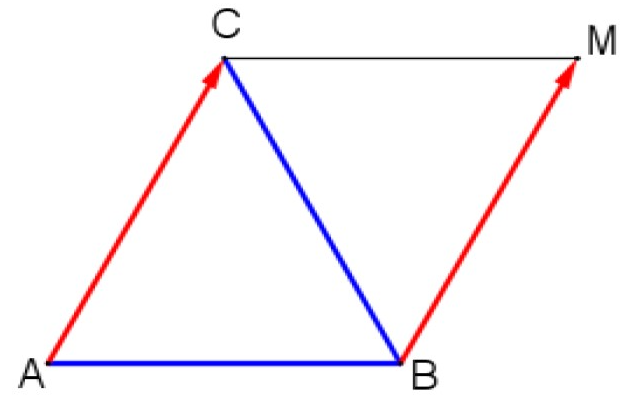
$3)$ Puisque $\overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{BM}}$ alors $ABMC$ est un parallélogramme.
$4)$-$a)$
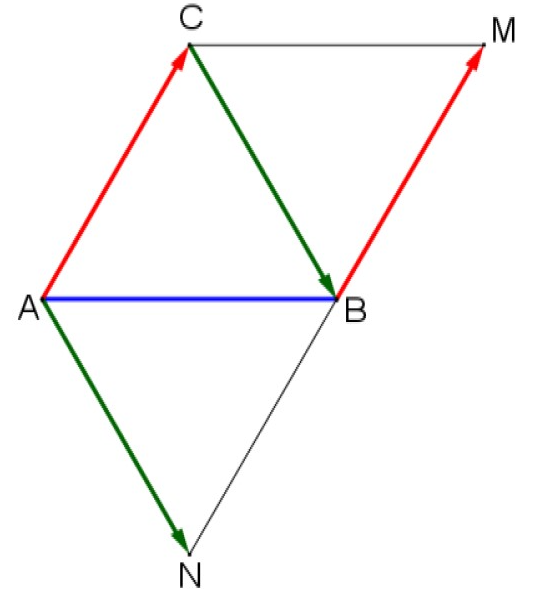
$b)$
On a : $\overrightarrow{\mathrm{CB}}=\overrightarrow{\mathrm{AN}}$
Donc $ACBN$ est un parallélogramme.
$\rightarrow$ ainsi : $\mathrm{AC}=\mathrm{BN}$ et $\mathrm{BC}=\mathrm{AN}$.
Or ABC est un triangle équilatéral, donc : $\mathrm{AB}=\mathrm{AC}=\mathrm{BC}$
En recoupant ces informations : $\mathrm{AB}=\mathrm{BN}=\mathrm{AN}$
Donc ABN est un triangle équilatéral.
Exercice 11:
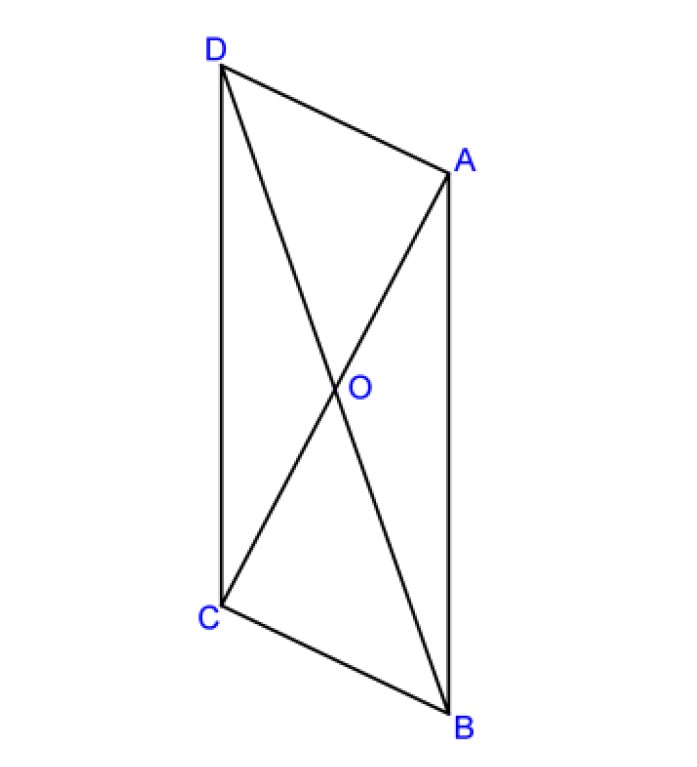
Sur cette figure, on a représenté un parallélogramme $ABCD$ de centre $O$ . Les droites v(BC)$ et $(AC)$ sont perpendiculaires.
$1)$ Tracer le cercle qui contient les trois points $O$, $B$ et $C$. Justifier la position de son centre $I$.
$2)$ Placer les points $M$ et $P$ tels que :
$\overrightarrow{\mathrm{OM}}=\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OC}} $
$\overrightarrow{\mathrm{BP}}=\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{OD}}$
$3)$ Utilisation d’une transformation.
$a)$ Par quelle transformation a-t-on à la fois: $O$ a pour image $C$ et $B$ a pour image $M$ ?
$b)$ Montrer que, par cette transformation, le point $D$ a pour image le point $P$ .
$c)$ Montrer que les point $\mathrm{P}, \mathrm{C}, \mathrm{M}$ sont alignés.
$1)$
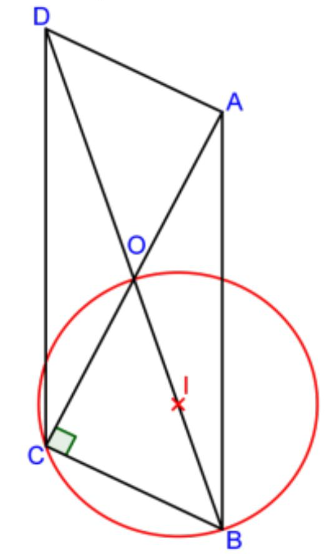
On sait que le triangle OBC est rectangle en C.
Dans un triangle rectangle, le milieu de l’hypoténuse est le centre du cercle circonscrit.
Donc I est le milieu de [OB].
$2)$
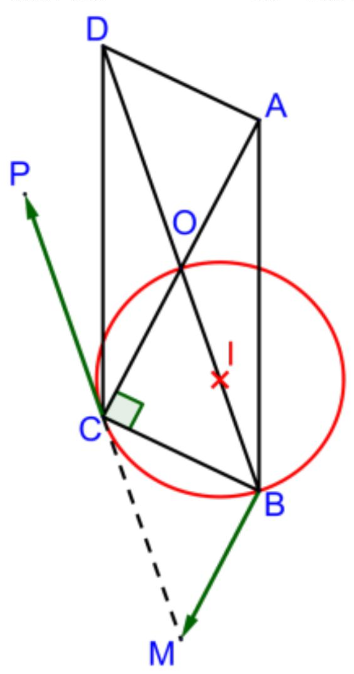
$3)$ Utilisation d’une transformation.
$a)$ La relation $\overrightarrow{\mathrm{OM}}=\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OC}}$ implique que le quadrilatère OBMC est un parallélogramme.
Ainsi $\overrightarrow{\mathrm{OC}}=\overrightarrow{\mathrm{BM}}$.
La transformation cherchée est une translation de vecteur $\overrightarrow{\mathrm{OC}}$.
$b)$ Montrer que, par cette transformation, le point $D$ a pour image le point $P$.
L’image d’une droite par une translation est une droite parallèle.
Donc l’image de la droite $(OB)$ est la droite $(CM)$.
De plus : $DO = OB = CP$
Le quadrilatère DOCP possède deux côtés parallèles et de même longueur: $DOCP$ est un parallélogramme, et $\overrightarrow{\mathrm{OC}}=\overrightarrow{\mathrm{DP}}$ : on reconnait translation de vecteur $\overrightarrow{\mathrm{OC}}$.
$c)$ Montrer que les point $\mathrm{P}, \mathrm{C}, \mathrm{M}$ sont alignés.
$DOCP$ , $OBMC$ et $ABCD$ sont 3 parallélogrammes, donc: $\quad \overrightarrow{\mathrm{DO}}=\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{CM}}=\overrightarrow{\mathrm{PC}}$
Ainsi les points $\mathrm{C}, \mathrm{M}$ et $P$ sont alignés.
Exercice 12:
Soit $[IJ]$ un segment et $M$ un point du cercle de diamètre $[IJ]$.
$1)$ Faire une figure.
$2)$ Que dire de l’angle $\widehat{I M J}$ ? Justifier.
$3)$ Construire le point $K$ tel que $\overrightarrow{\mathrm{MK}}=\overrightarrow{\mathrm{IM}}$.
$4)$ Construire le point $L$ tel que $\overrightarrow{\mathrm{JL}}=\overrightarrow{\mathrm{JI}}+\overrightarrow{\mathrm{JK}}$.
$5)$ Déterminer la nature du quadrilatère $IJKL$.
$1)$
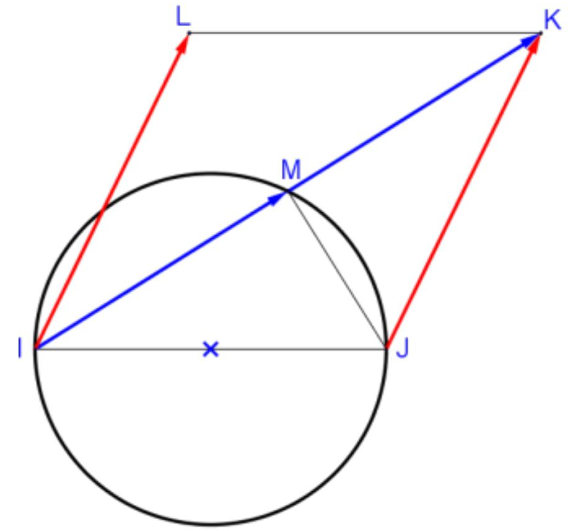
$2)$ Les points $I, J, M$ sont sur un cercle de diamètre $[IJ]$. Si trois points sont sur un cercle et si deux de ces points sont les extrémités d’un diamètre de ce cercle, ce triangle est rectangle et ce diamètre est son hypoténuse.
Donc le triangle $IJM$ est rectangle en $M$.
$3)$ Sur la figure
$4)$ Sur la figure
$5)$ Par construction, $M$ est le milieu de la diagonale $[IK]$ du quadrilatère $IJKL$.
Par construction: $\overrightarrow{\mathrm{IL}}=\overrightarrow{\mathrm{JK}}$ donc le quadrilatère $IJKL$ est un parallélogramme.
Exercice 13:
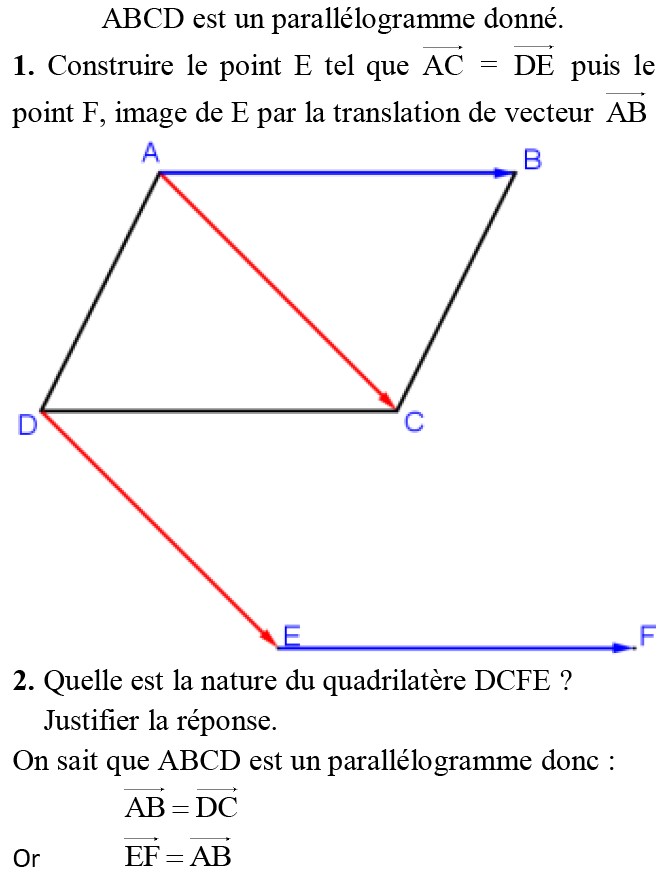
$ABCD$ est un parallélogramme donné.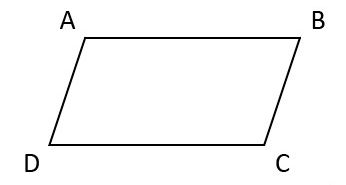
$1)$ Construire le point $E$ tel que $\overrightarrow{A C}=\overrightarrow{D E}$ puis le point $F$, image de $E$ par la translation de vecteur $\overrightarrow{A B}$
$2)$ Quelle est la nature du quadrilatère $DCFE$ ? Justifier la réponse.
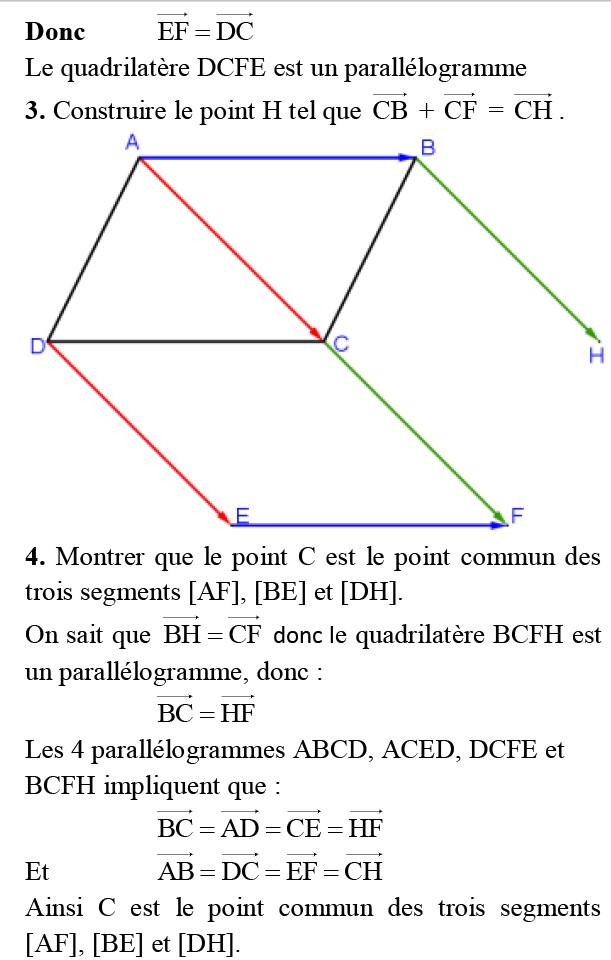
$3)$ Construire le point $H$ tel que : $\overrightarrow{\mathrm{CB}}+\overrightarrow{\mathrm{CF}}=\overrightarrow{\mathrm{CH}}$.
$4)$ Montrer que le point $C$ est le point commun des trois segments $[AF]$, $[BE]$ et $[DH]$.
$1)$
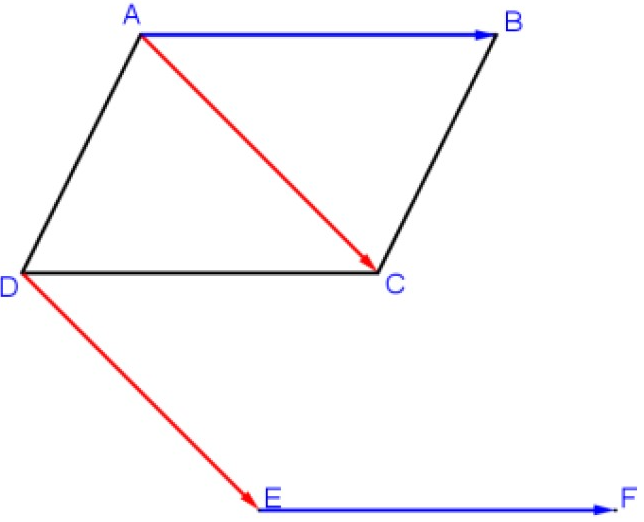
$2)$ On sait que $A B C D$ est un parallélogramme
Donc : $\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{DC}}$
Or $\quad \overrightarrow{\mathrm{EF}}=\overrightarrow{\mathrm{AB}}$
Donc $\quad\overrightarrow{\mathrm{EF}}=\overrightarrow{\mathrm{DC}}$
D’ou le quadrilatère $DCFE$ est un parallélogramme.
$3)$
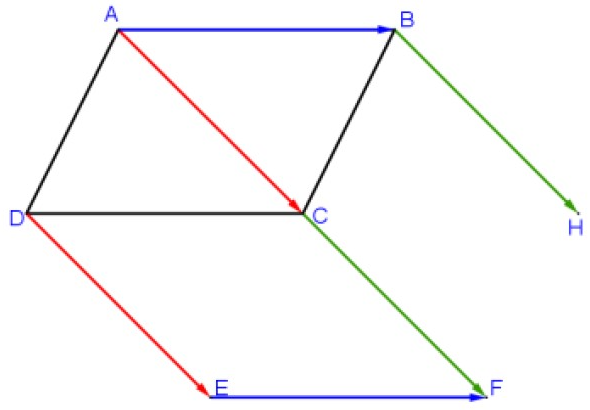
$4)$
On sait que $\overrightarrow{\mathrm{BH}}=\overrightarrow{\mathrm{CF}}$ donc le quadrilatère $BCFH$ est un parallélogramme
Donc : $\overrightarrow{\mathrm{BC}}=\overrightarrow{\mathrm{HF}}$
Les 4 parallélogrammes $ABCD$ , $ACED$, $DCFE$ et $BCFH$ impliquent que :
$\overrightarrow{\mathrm{BC}}=\overrightarrow{\mathrm{AD}}=\overrightarrow{\mathrm{CE}}=\overrightarrow{\mathrm{HF}} $ et $\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{DC}}=\overrightarrow{\mathrm{EF}}=\overrightarrow{\mathrm{CH}}$
Ainsi $C$ est le point commun des trois segments $[AF]$, $[BE]$ et $[DH]$.
Vecteurs et translation 2AC exercices corrigés