Introduction :
Dans le vaste royaume de la géométrie, les angles occupent une place centrale, offrant un langage visuel pour décrire les relations spatiales.Parmi eux, l’angle vertical se distingue par sa simplicité apparente et sa présence ubiquitaire dans diverses configurations géométriques.
Dans cet article, nous plongerons dans la signification et les propriétés de cet angle , explorant son rôle essentiel dans la compréhension de l’espace.
Définition de l’Angle Vertical :
L’angle est formé par deux lignes droites qui se croisent. Plus spécifiquement, ces lignes droites sont opposées l’une à l’autre, créant ainsi deux paires d’angles égaux. Lorsque deux lignes se croisent, les angles opposés sont toujours congruents, c’est-à-dire qu’ils ont la même mesure.
Dans les cours de topométrie cet angle est appelé indifféremment :
♦ Angle vertical de A vers B
♦ Angle zénithal de A vers B
♦ Distance zénithale de A vers B
♦ Zénithale de A vers B
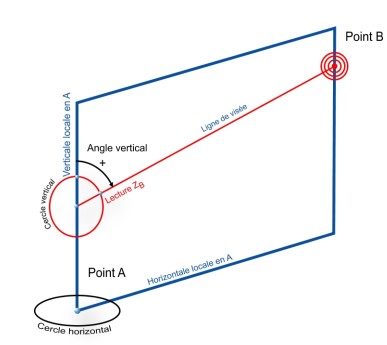
Propriétés de l’Angle Vertical :
Congruence des Angles Opposés :
L’une des propriétés fondamentales de cet angle est que les angles opposés sont égaux en mesure. Si l’angle A est opposé à l’angle B, alors mes(A) = mes(B).
Formation dans les Intersections :
Les angles verticaux se forment chaque fois que deux lignes droites se croisent. Que ce soit dans des figures simples ou dans des configurations complexes, les angles verticaux émergent naturellement à ces intersections.
Utilité dans la Résolution de Problèmes :
En raison de la congruence des angles opposés, cet angle est souvent utilisé pour résoudre des problèmes géométriques. En connaissant la mesure de cet angle, on peut déduire la mesure de l’angle opposé.
Applications Pratiques de l’Angle Vertical :
Construction et Architecture :
Les professionnels de la construction et de l’architecture utilisent fréquemment cet angle pour garantir la précision des angles dans la conception et la construction de structures.
Cartographie et Navigation :
En cartographie et navigation, où la précision des angles est cruciale, l’angle est un outil précieux pour déterminer la direction et la position relative.
Conclusion :
L’angle vertical, simple en apparence, joue un rôle essentiel dans la géométrie et au-delà. Sa congruence constante offre une règle précieuse pour comprendre les relations angulaires dans des contextes variés.
Que ce soit dans la construction, la cartographie ou la résolution de problèmes mathématiques, l’angle se présente comme une boussole fiable, nous guidant à travers les dédales de l’espace géométrique.
En appréciant l’importance de cet angle, nous enrichissons notre compréhension de la géométrie et de son impact pratique dans le monde qui nous entoure.
