Calcul litteral 3eme et identités remarquables

I . Développement:

1-Définition :

Développer un produit signifie le transformer en une somme algébrique .

2-Propriétés

Propriété 1 :

Soient $a, b$ et $k$ des nombres décimaux relatifs on a :

$ k \times(a+b)=k \times a+k \times b$

$ k \times(a-b)=k \times a-k \times b$

Exemples :

$ 3(5 a+7)=3 \times 5 a+3 \times 7  =15 a+21$

$ \sqrt{5}(\sqrt{5}-1)=\sqrt{5} \times \sqrt{5}-\sqrt{5} \times 1 =\sqrt{5}^{2}-\sqrt{5}=5-\sqrt{5}$

Propriété 2 :

$a , b , c$ et d sont des nombres réels.

On a : $(a + b)(c + d) = ac + ad + bc + bd$

Exemple :

$(3-a)(4 a+2)  =3 \times 4 a+3 \times 2-a \times 4 a-a \times 2 =12 a+6-4 a^{2}-2 a=-4 a^{2}+10 a+6$

II. Factorisation :

Définition :

Factoriser une somme algébrique signifie la transformer en produit.

Règle :

Soient a, b et k des nombres décimaux relatifs on a :

$k \times a+k \times b=k \times(a+b)$

$k \times a-k \times b=k \times(a-b)$

Exemples :

$ 4 a^{2}+3 a=4 \times a \times a+3 \times a=a(4 a+3) $

$ (x+7)(5-4 x)-2(5-4 x)=(5-4 x) \times(x+7-2)=(5-4 x)(x+5) $

$ (x+3)^{2}+(x+4)(x+3)=(x+3)(x+3+x+4)=(x+3)(2 x+7)$

III. Identités remarquables

1 -Carré d’une somme

Propriété  :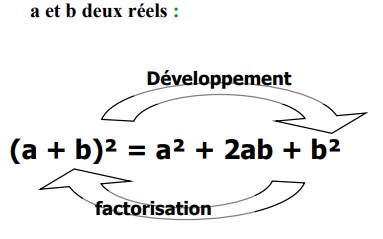 

Exemples :

$ (2 x+3)^{2}=(2 x)^{2}+2 \times 2 x \times 3+3^{2}=4 x^{2}+12 x+9 $

$ 16 x^{2}+8 x+1=(4 x+1)^{2} $

$ 25 x^{2}+20 x+4=(5 x+2)^{2}$

2-Carré d’une différence

Propriété  :

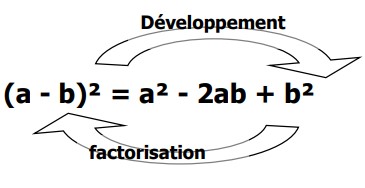
Exemples :

$(2 x-3)^{2}=(2 x)^{2}-2 \times 2 x \times 3+3^{2}=4 x^{2}-12 x+9$

$ 99^{2}=(100-1)^{2}=100^{2}-2 \times 100 \times 1+1^{2}=10000-200+1=9801$

$ 16 x^{2}-8 x+1=(4 x-1)^{2}$

3- Produit d’une somme par une différence

Propriété  :

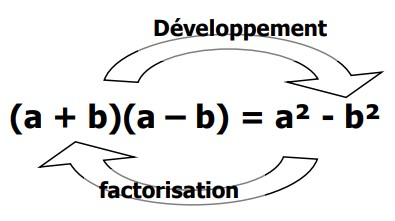
Exemples :

$ (2 x+3)(2 x-3)=(2 x)^{2}-3^{2}=4 x^{2}-9 $

$ \quad 99 \times 101=(100+1)(100-1)=100^{2}-1^{2}=10000-1=9999$

$ (\sqrt{11}+\sqrt{7})(\sqrt{11}-\sqrt{7})=\sqrt{11}^{2}-\sqrt{7}^{2}=11-7=4$

$ 16 x^{2}-9=(4 x+3)(4 x-3) $