Il vaut mieux essayer de faire les exercices avant de commencer à regarder les réponses

ℵ Droite graduée et repérage dans le plan_Cours

ℵ Droite graduée et repérage dans le plan_Exercices corrigés_1

ℵ Droite graduée et repérage dans le plan_Exercices corrigés_2

ℵ Droite graduée et repérage dans le plan_Exercices corrigés_3

ℵ Droite graduée et repérage dans le plan_Exercices corrigés_4

Voici un rappel du cours de la droite graduée et repérage dans le plan

Droite graduée et repère dans le plan

1.1  droite graduée et repérage dans le plan

La droite ci-dessus est graduée : elle a une origine O, une unité OI et la distance OI est reportée régulièrement à gauche et à droite à partir de O. A chaque point de la droite est associé un nombre, son abscisse, qui donne sa position par rapport à O.
L’abscisse de A est +3, on pourra la noter xA
L’abscisse de B est –4, on pourra la noter xB

Exemples : 

Donner une feuille sur laquelle il y a une droite graduée et des points (abscisses entières et décimales) à lire et une droite graduée sur laquelle il faut placer des points dont l’abscisse (entière et décimale) est donnée.

1.2 Repérage dans le plan

Deux droites graduées perpendiculaires de même origine constituent un repère du plan.
La droite « horizontale » est appelée axe des abscisses.
La droite « verticale » est appelée axe des ordonnées.

Chaque point du plan peut alors être repéré par deux nombres appelés coordonnées du point.
La première coordonnée, appelée abscisse, est lue sur l’axe des abscisses.
La seconde coordonnée, appelée ordonnée, est lue sur l’axe des ordonnées.

Exemples :

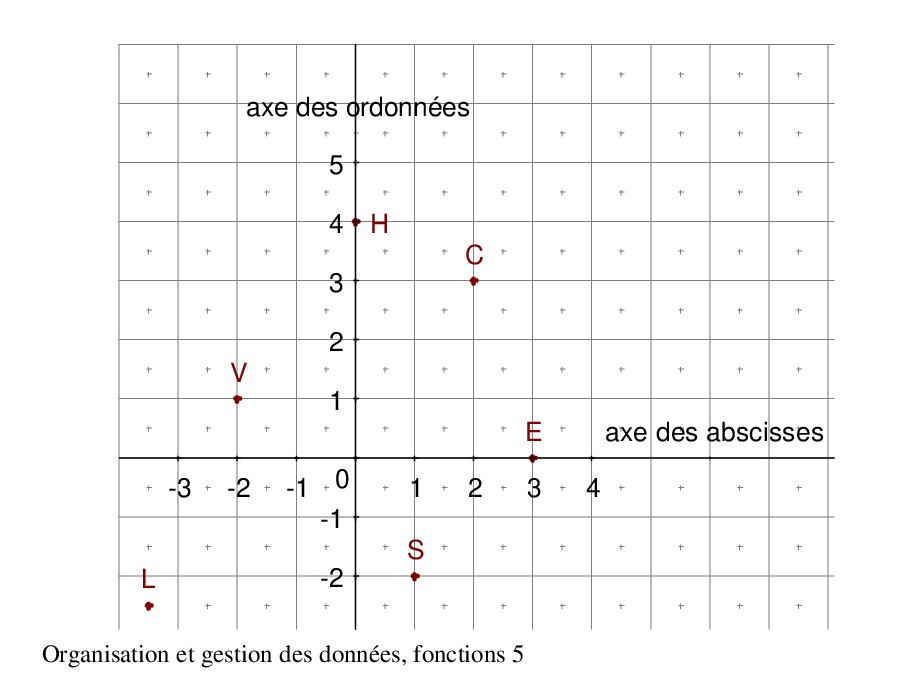
Les coordonnées de C sont (2 ;3). 2 est l’abscisse, 3 est l’ordonnée. On pourra écrire xC = 2 et  yC = 3
V (-2 ;1)
S (1 ;-2)
E (3 ;0)
H (0 ;4)
L (-3,5 ;-2,5)

Remarque :

La droite graduée et repérage dans le plan est constitué de deux partie comme nous l’avons vu.

les unités sur les axes peuvent être différentes (voir exercices)

Vous allez trouver ci-dessous des exercices corrigés de la droite graduée et repérage dans le plan

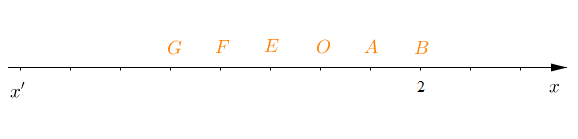
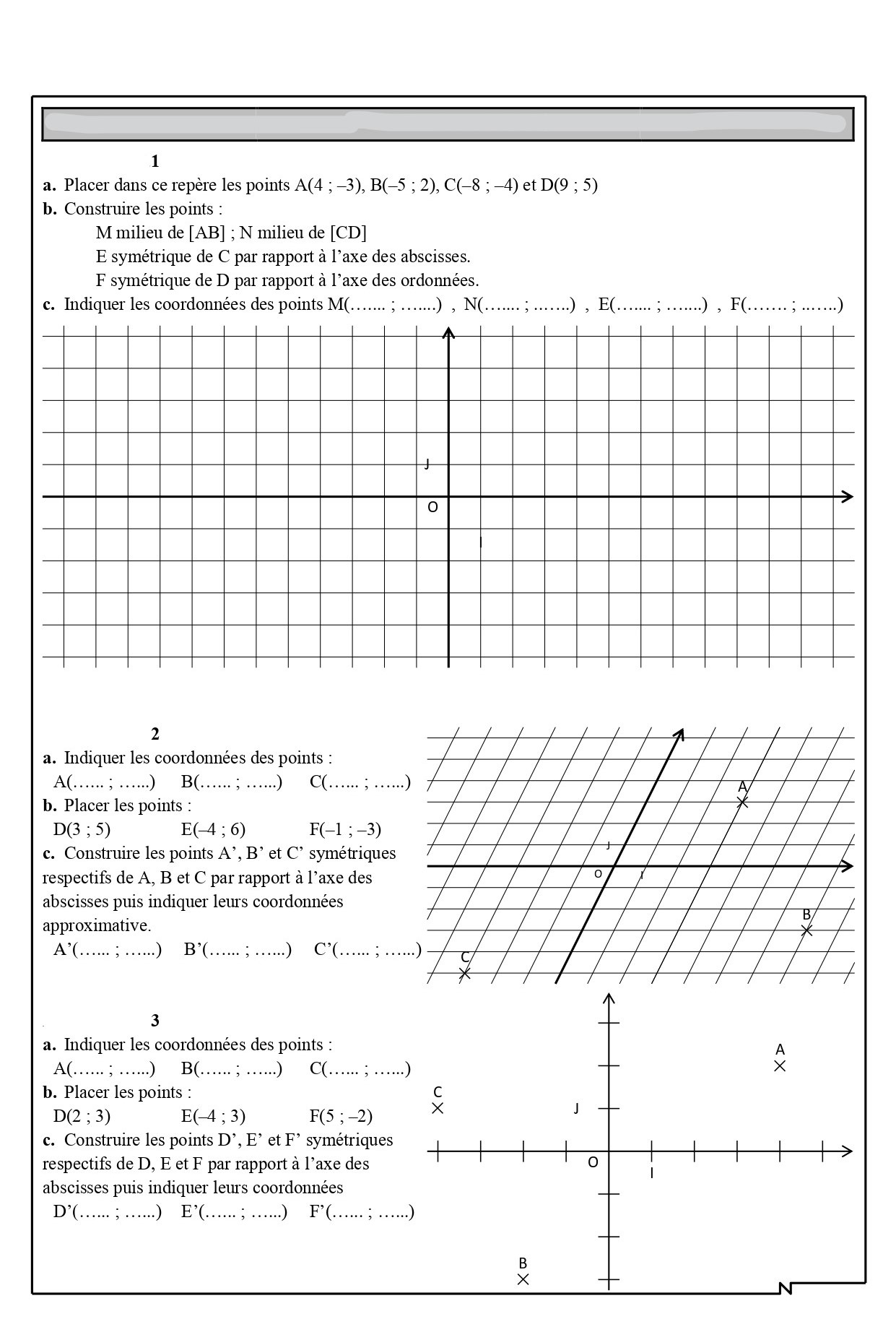
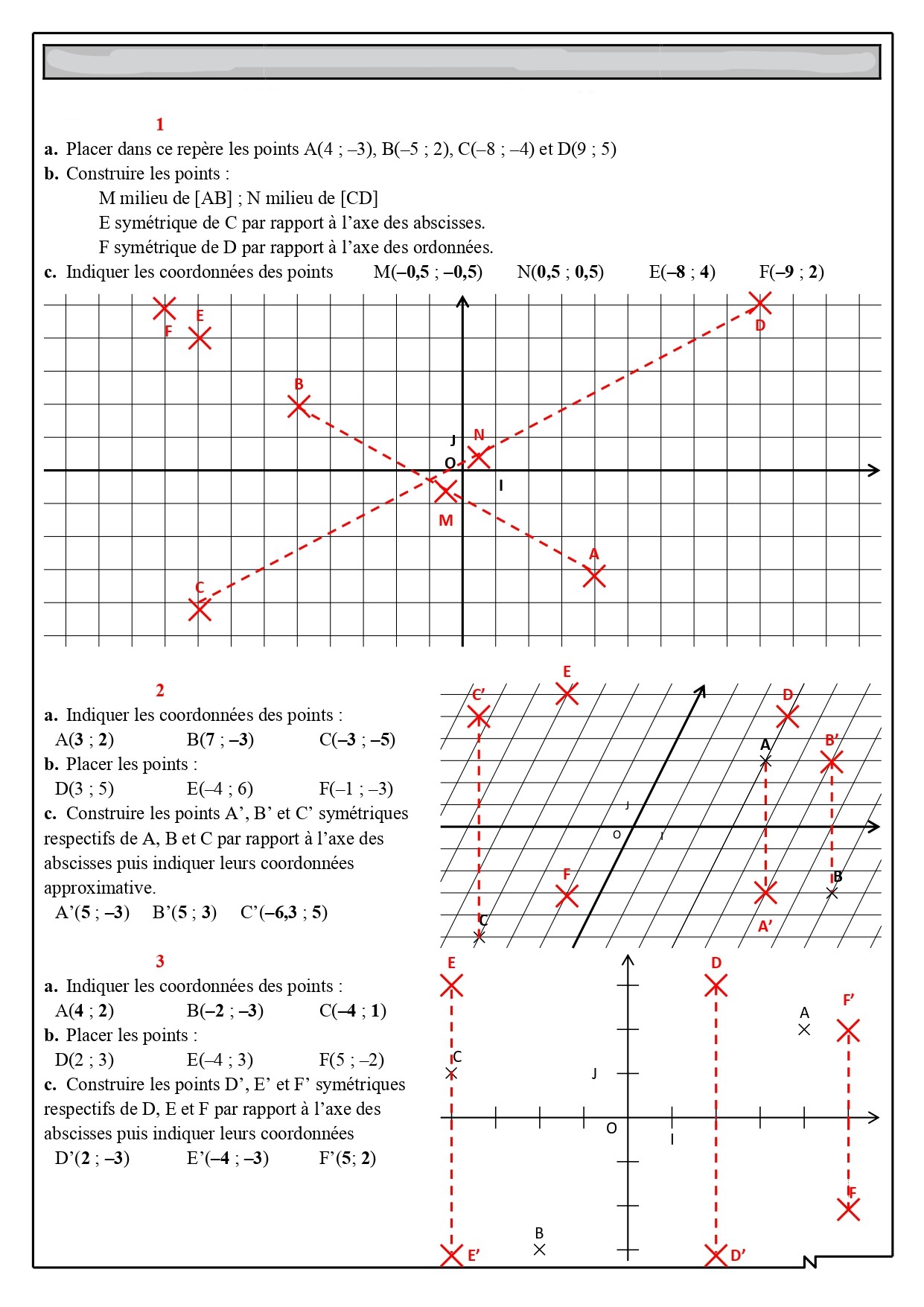
1) A quelles abscisses correspondent les points  et  


 

 

2) Calculer les distances : ;   et  OG.


3) Calculer les distances : ;   et 

Repère dans le plan

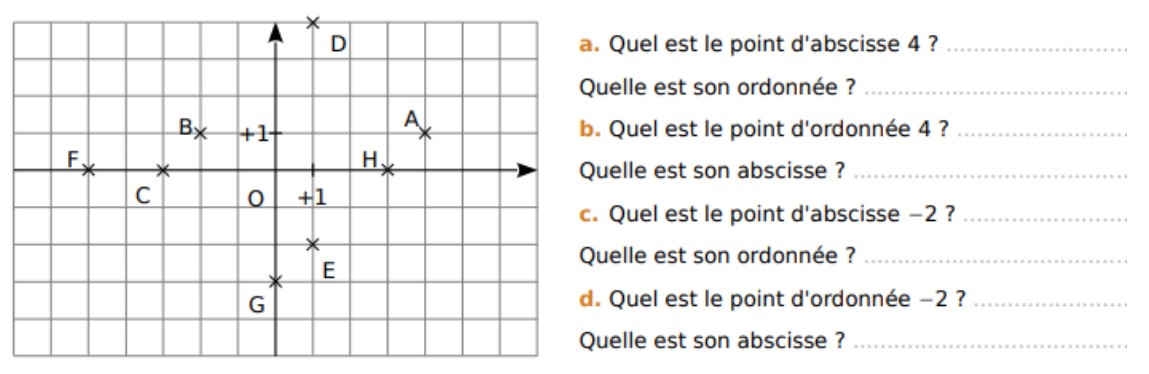
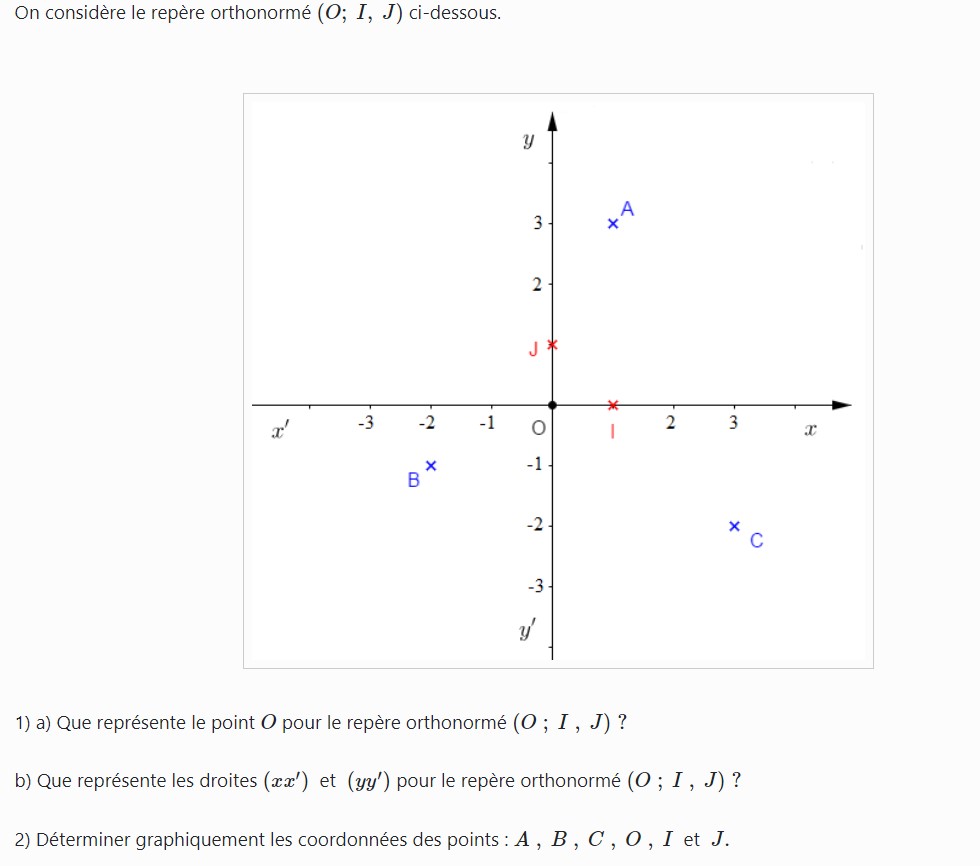
On considère la figure ci-dessous :

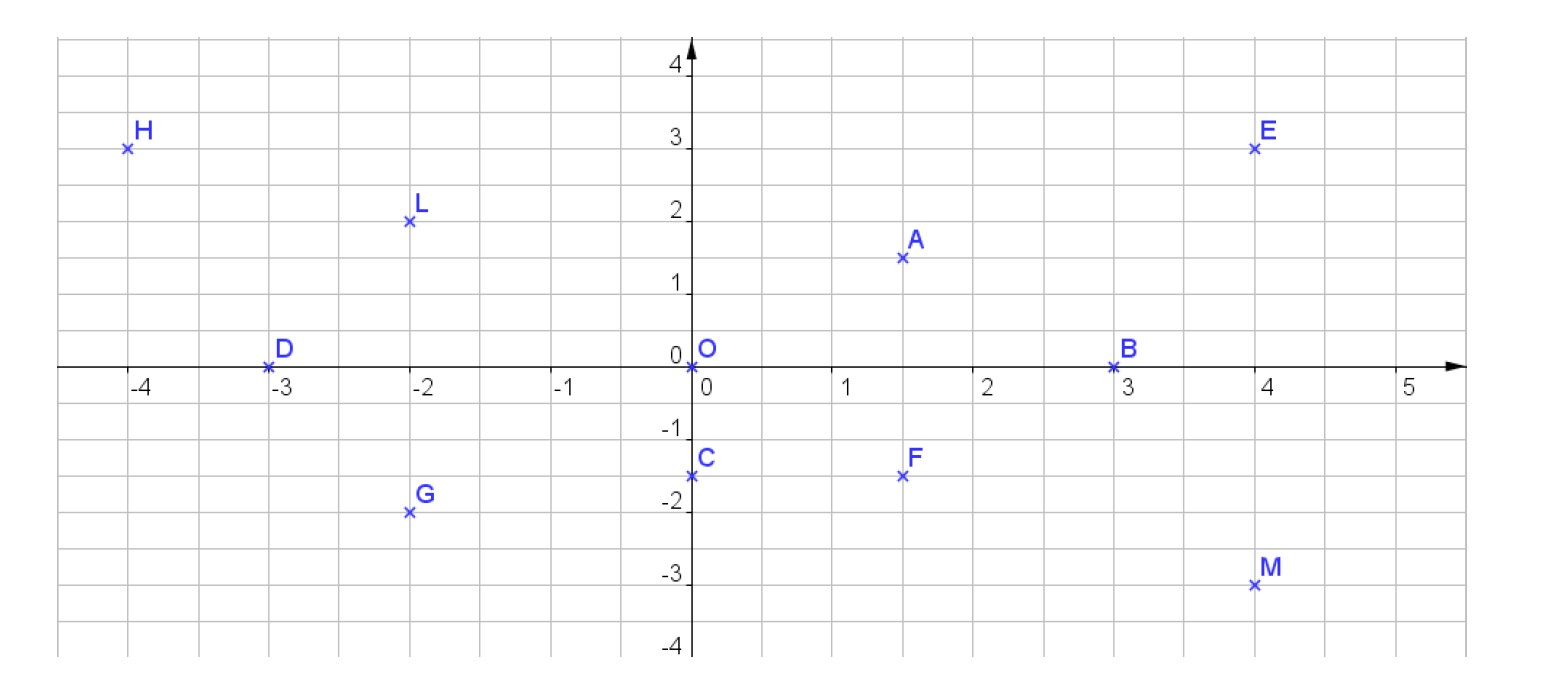
1. Compléter les phrases suivantes :
Le point O est ……………………………. du repère Sur l’axe horizontal, on peut lire les …………………………………….. et sur l’axe vertical, on peut lire les ………………………………………

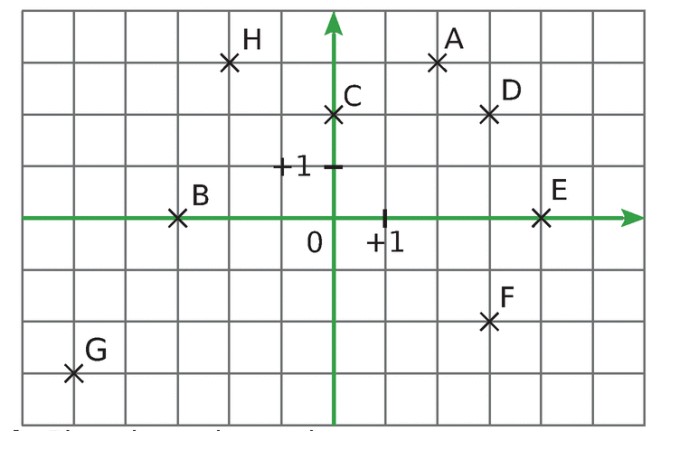
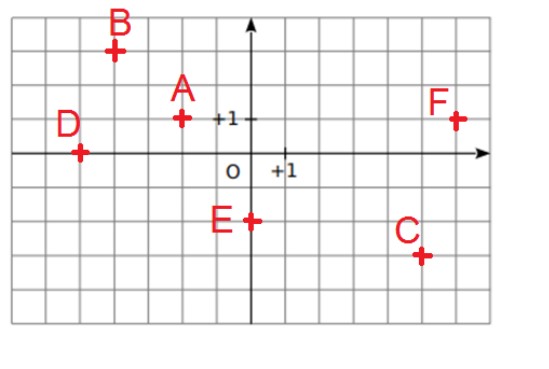
2. Quelles sont les coordonnées de chacun des points : O, A, B, C, D, E, F, G, H, L et M ?

3. Parmi les points de la figure, le ou lesquels :
   a. ont la plus grande abscisse ? Laquelle ?
   b. ont la plus petite abscisse ? Laquelle ?
   c. ont la plus grande ordonnée ? Laquelle ?
   d. ont la plus petite ordonnée ? Laquelle ?

4. Parmi les points de la figure, lesquels :
   a. ont l’abscisse comprise entre –3,5 et 1 ?
   b. ont l’ordonnée comprise entre –2,5 et 0,5 ?

5. Parmi les points de la figure, lesquels :
   a. ont la même abscisse ?
   b. ont la même ordonnée ?

6. Parmi les points de la figure, lesquels :
   a. ont des abscisses opposées ?
   b. ont des ordonnées opposées ?
   c. ont à la fois des abscisses opposées et des ordonnées opposées ?

7. Parmi les points de la figure, lesquels :
   a. ont l’abscisse égale à l’ordonnée ?
   b. ont l’abscisse et l’ordonnée opposées ?

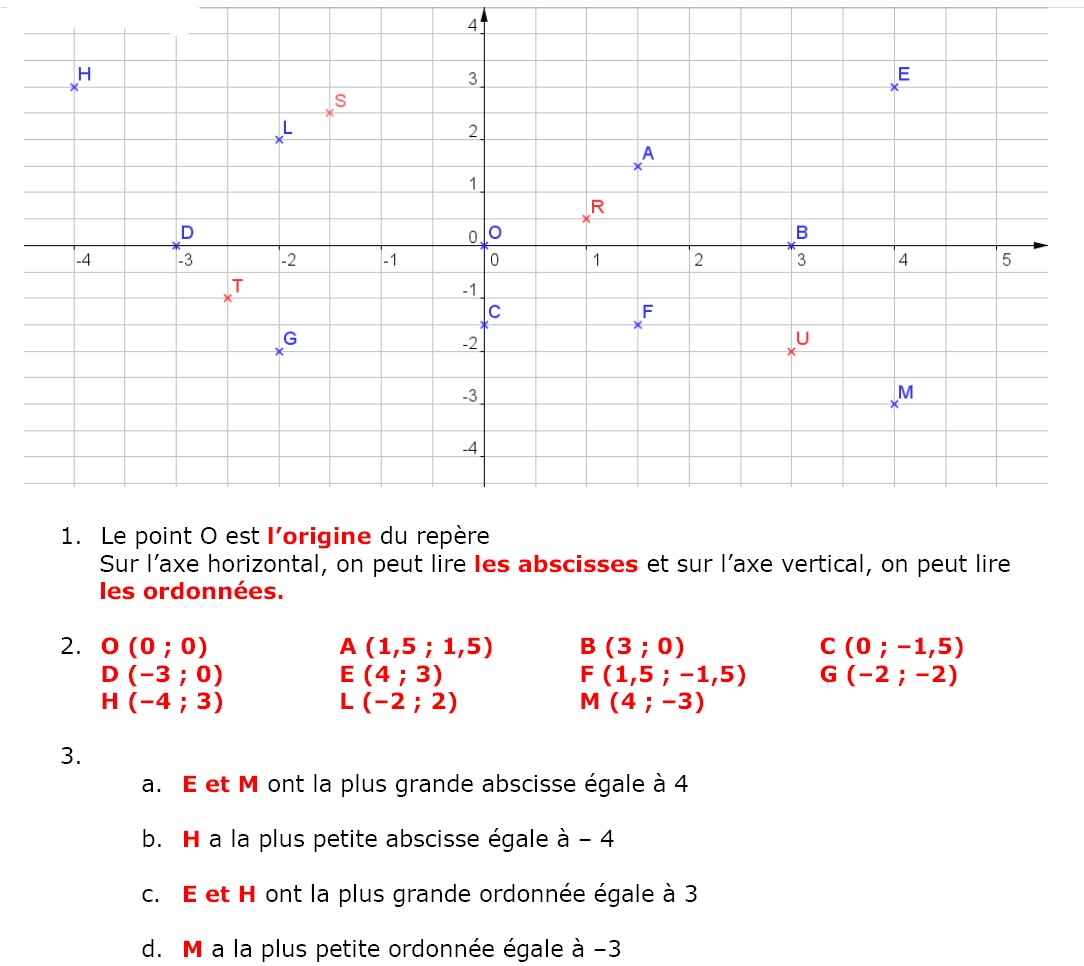
8. Placer les points R, S, T, U de coordonnées respectives : (1 ; 0,5), (–1,5 ; 2,5), (–2,5 ; –1) et (3 ; –2)

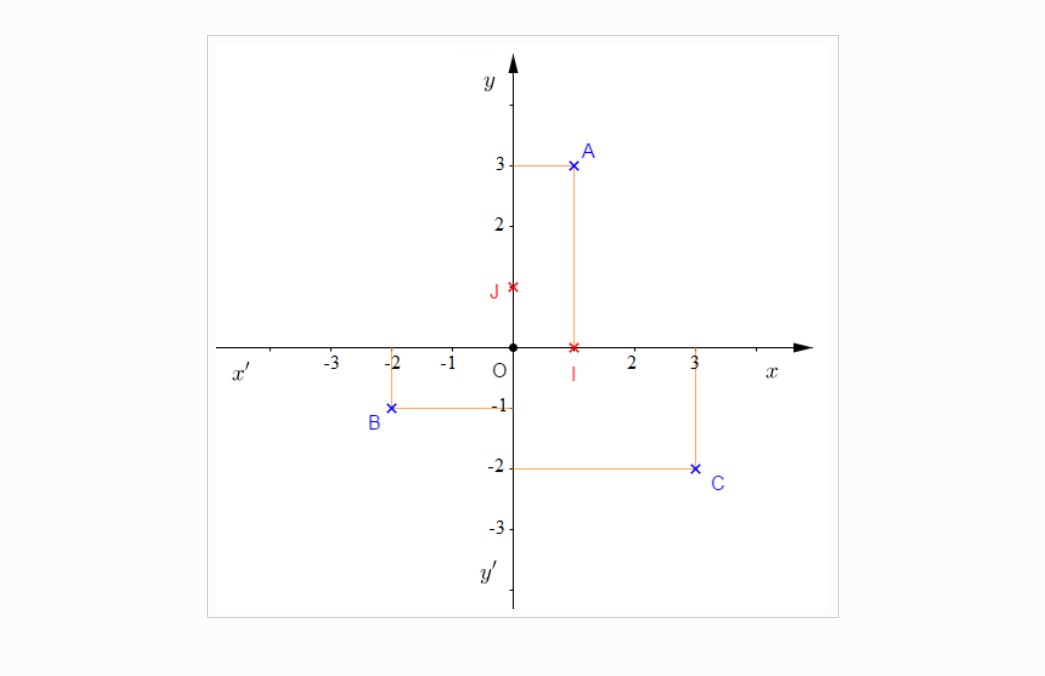
1) Compéter en-dessous du graphique les coordonnées des différents points.

 

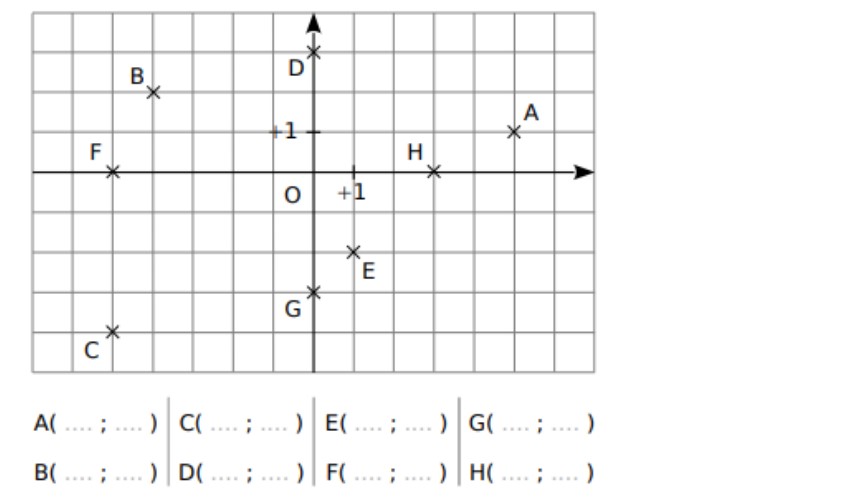
2) Ecrire en-dessous du graphique les coordonnées des différents points.

1)

𝐴(5; 1) ; 𝐵(−4; 2) ;  𝐶(−5; −4) ; 𝐷(0; 3) ; 𝐸(1; −2) ; 𝐹(−5; 0) ; 𝐺(0; −3) ; 𝐻(3; 0)

2) 
𝐴(2; 3) ; 𝐵(−3; 0) ;  𝐶(0; 2) ; 𝐷(3; 2) ; 𝐸(4; 0) ; 𝐹(3; −2) ; 𝐺(−5; −3) ; 𝐻(−2; 3)

a. le point A

    Son ordonnée est 1.

b. le point D

    Son abscisse est 1.

c. le point B

   Son ordonnée est 1.

d. le point E

    Son abscisse est 1.