identités remarquables cours

En mathématiques, on appelle identités remarquables les égalités qui s’appliquent à des nombres. Elles les utilisent généralement pour accélérer les calculs, pour simplifier les écritures, ainsi pour factoriser ou  développer des expressions.

les identités remarquables sont les expressions mathématiques qui sert à faire le calcul littéral. Les identités remarquables sont utiles pour résoudre les équations. Comment utilise-t-on ses identités remarquables ?  Comment développer ou factoriser une expression ?  Découvrez tout ce que vous devez savoir.

1.  Identités remarquables

a et b sont des expressions littérales ou des nombres. Alors :

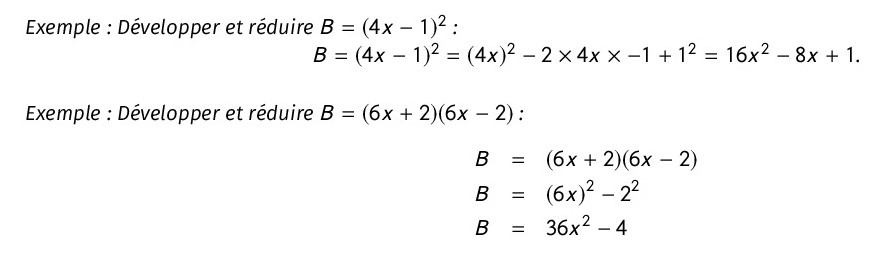
Faites ces exercices pour bien comprendre le cours: 

:

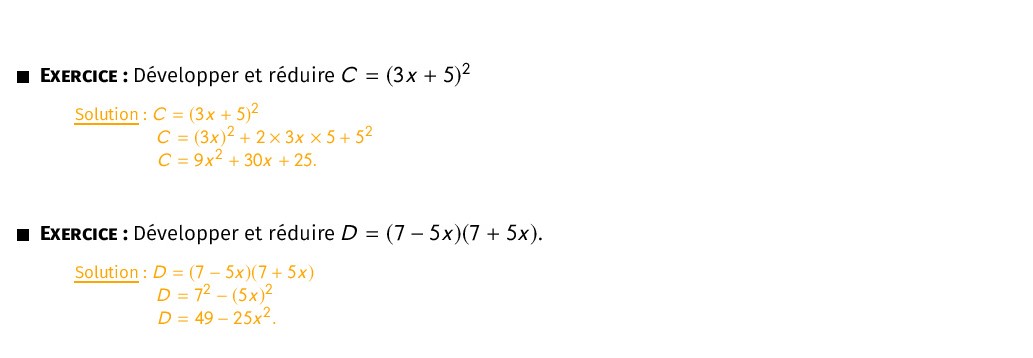
Factoriser en utilisant une identité remarquable est un peu plus délicat. On va détailler selon l’identité remarquable à
utiliser : 1er type de factorisation puis le 2ème type de factorisation

Alors là vous faites attention à la racine carrée:

2. Développement

1.Développement par la distributivité

Propriété
soient a, b, c, d et k des nombres réels Développer un produit c’est le transformer en une somme ou une différence
algébrique tels que:
k(a + b) = ka + kb
k(a − b) = ka − kb
(a + b)(c + d) = a(c + d) + b(c + d) = ac + ad + bc + bd

3.Factorisation

1.Factorisation par le facteur commun

Propriété
soient a, b et k des nombres réels
factoriser une somme c’est le transformer en produit tels que :
ka + kb = k(a + b)
ka − kb = k(a − b)
K est appelé le facteur commun