La droite et ses parties
Exercice 1:
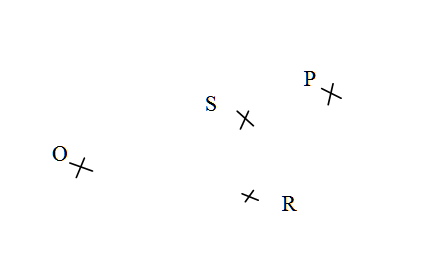
$1)$Tracer au crayon noir la droite $(OP)$.
$2)$Tracer en rouge le segment $[OR]$.
$3)$Mesurer la longueur du segment $[OR]$ :
$OR = ………….$
$4)$ Placer le point $I$ milieu du segment $[OR]$ :
Alors : $OI = IR = ……….$
$5)$Les points $O$, $S$ et $P$ sont ………..
Les points $O$, $S$ et $R$ ne sont pas ……….
$6)$Compléter à l’aide des symboles $∈$ ou $∉$ :
$R …. (OP)$
$O …. (SP)$
$O ….[SP]$
$P ….[SO)$
$1)$ et $2)$
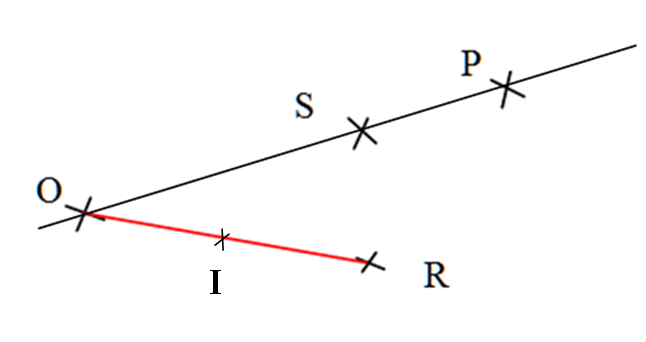
$3)$ $OR = 4 cm $
$4)$ Placer le point $I$ milieu du segment $[OR]$ :
Alors : $OI = IR = 2 cm$
$5)$ Les points O, S et P sont alignés
Les points O, S et R ne sont pas alignés
$6)$ Compléter à l’aide des symboles $∈$ ou $∉$ :
$R ∉ (OP)$
$O ∈ (SP)$
$O ∉ [SP]$
$P ∉ [SO)$
Exercice 2:
Après avoir observé la figure ci-dessous, recopie et complète les pointillés en utilisant $∈$ ou $∉$ :

$M … [AC]$ $L … [CM)$
$L … (AM)$ $P… [AL]$
$P … (AL)$ $A … [LC)$
$A … (ML)$ $ A … [AM]$
Exercice 3:
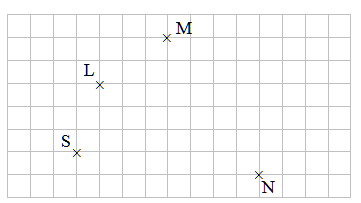
$1)$ Reproduis cette figure sur ta copie en respectant le nombre de carreaux.
$2)$ Les droites $(LN)$ et $(MS)$ sont sécantes en $O$. Place $O$.
$3) $Le point d’intersection des droites $(LM)$ et $(SN)$ est le point $R$. Place $R$.
$4)$ Les points $L$, $S$ et $T$ sont alignés ainsi que les points $M$, $N$ et $T$. Place $T$.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 4:
En utilisant tes instruments de géométrie, indique par un codage les droites qui sont perpendiculaires :
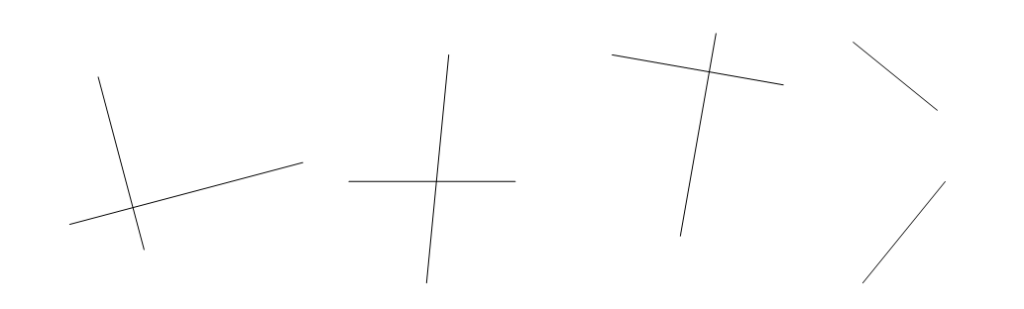
Exercice 5:
$1)$ Dessine deux droites $(xy)$ et $(uv)$ sécantes en $F$ et qui ne sont pas perpendiculaires.
$2)$ Dessine deux droites $(D)$ et $(D’)$ perpendiculaires.Appelle $E$ leur point d’intersection.
Exercice 6:
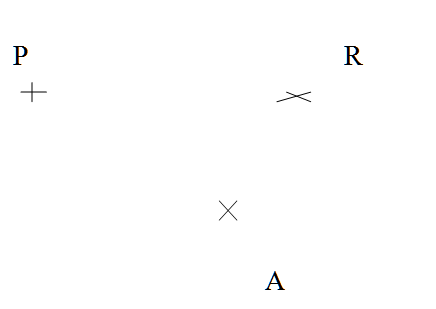
$1)$ Trace en rouge la droite $(AP)$.
$2)$ Trace en vert la droite $(AR)$.
$3)$ Vérifie avec ton équerre qu’il y a un angle droit. Indique-le sur le dessin.
Exercice 7:
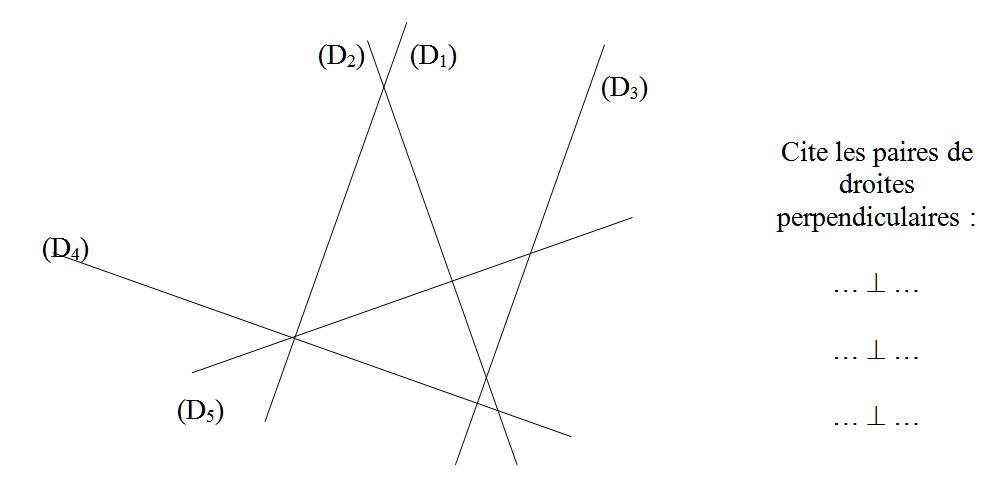
Sur le dessin ci-dessous, on a tracé cinq droites.
Cherche à l’aide de tes instruments de géométrie celles qui sont perpendiculaires.
Exercice 8:
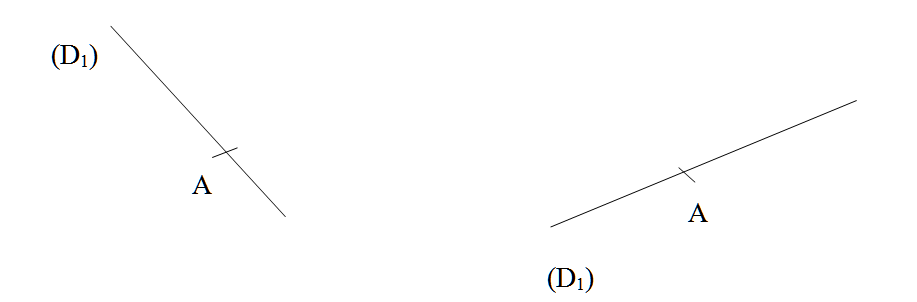
Sur chaque dessin, trace à l’aide de tes instruments de géométrie, la droite (D2) perpendiculaire en $A$ à la droite (D1).
Exercice 9:
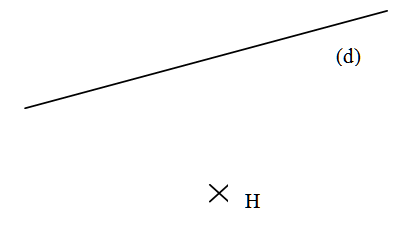
$1)$ Tracer la droite $(d’)$ parallèle à la droite $(d)$ passant par $H$.
$2)$ Tracer la droite $( d_{1})$ parallèle à la droite $(Δ)$ passant par $A$, et la droite $( d_{2})$ perpendiculaire à la droite $(Δ)$ passant par $A$.
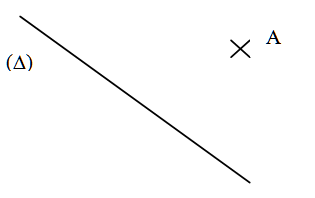
- Que peut-on dire de $( d_{1})$ et $( d_{2})$ ?
$3)$ Tracer la droite $(\Delta_{1})$ perpendiculaire à la droite $(d)$ passant par $A$, et la droite $(\Delta_{1})$ perpendiculaire à la droite $(d)$ passant par$ B$.
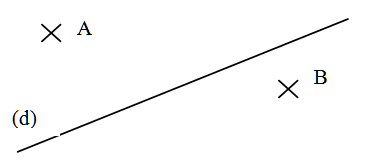
- Que peut-on dire de $(\Delta_{1})$ et $(\Delta_{2})$ ?
Exercice 10:
$1)$ Trace un triangle $ABC$ tel que $AB = 5 cm$ ; $AC = 8 cm$ et $BC = 10 cm$.
$2)$ Trace la droite $(d)$ parallèle à $(BC)$ passant par $A$.
$3)$ Trace la droite $(d’)$ perpendiculaire à $(BC)$ passant par $B$.
$4)$ On note I le point d’intersection des droites $(d)$ et $(d’)$.
$5)$ Place le point $D$ tel que I soit le milieu du segment $[AD]$.
$6)$ Place le point $E$ tel que $ABED$ soit un losange.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
La droite et ses parties
