La masse volumique exercices corrigés
❖ Expérience :
On mesure les masses de volumes différents d’un liquide (huile de table)
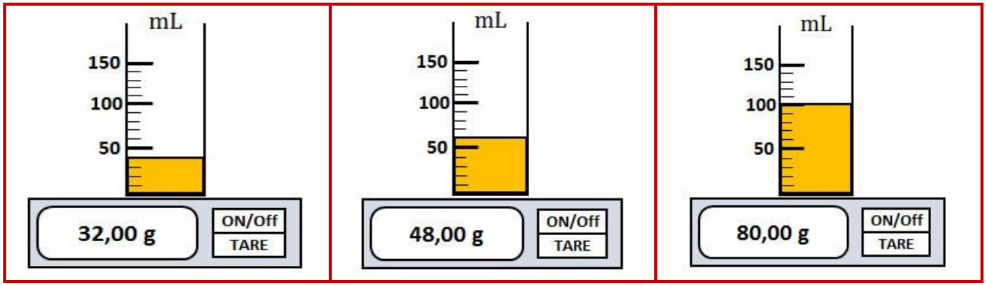
❖ Résultats :
| La masse en (g) | 32 | 48 | 80 |
|---|---|---|---|
| Le volume en (mL) | 40 | 60 | 100 |
| m/v en (g/mL) | 0,8 | 0,8 | 0,8 |
- ▪ Le rapport m/v reste constant quel que soit le volume du liquide.
- ▪ Le rapport m/v s’appelle la masse volumique de la matière.
❖ Conclusion :
- ▪ La masse volumique d’une matière est la masse de l’unité de volume de cette matière, on la note par la lettre ρ.
- ▪ Dans le système international, l’unité de la masse volumique est (Kg/m³).
- ▪ L’unité usuelle de la masse volumique est (g/mL).
- ▪ Pour calculer la masse volumique d’une matière on applique la relation suivante :
❖ La masse volumique de quelques matières
| La matière | eau | fer | Or | Huile d’olive | cuivre |
|---|---|---|---|---|---|
| ρ en (g/mL) | 1 | 7,86 | 19,3 | 0,82 | 8,92 |
Exercice 1:
Placer les mots suivants dans la bonne place : $\rho=\frac{m}{V}$, petite, kilogramme, mètre cube, grande, rho, $\rho$.
– La masse volumique d’une matière est la masse par unité de volume, notée $……….$ qui se prononce $……….$ et s’exprime selon la relation suivante : $……….$
– l’unité internationale de la masse volumique est le $……….$ par $……….$ ( $\mathrm{Kg} / \mathrm{m}^{3}$ ).
– Un objet flotte sur un liquide si sa masse volumique est plus $……….$ que celle du liquide.
– Un objet coule sur un liquide si sa masse volumique est plus $……….$ que celle du liquide.
– La masse volumique d’une matière est la masse par unité de volume, notée $\rho$ qui se prononce rho et s’exprime selon la relation suivante : $\rho=\frac{m}{V}$
– L’unité internationale de la masse volumique est le kilogramme par mètre cube ( $\mathrm{Kg} / \mathrm{m}^{3}$ ).
– Un objet flotte sur un liquide si sa masse volumique est plus petite que celle du liquide.
– Un objet coule sur un liquide si sa masse volumique est plus grande que celle du liquide.
La masse volumique exercices corrigés
Exercice 2:
Les objets flottant sur l’eau sont ceux pour lesquels la masse volumique est inférieure à $1 \mathrm{~g} / \mathrm{cm}^{3}$. Complète le tableau ci-dessous et indique quels objets flottent sur l’eau.
$\begin{array} {|r|r|}\hline Matériau & fer & liège & sapin & diamant & acajou \\ \hline \mathrm{m}(\mathrm{g}) & 393 & 48 & 45 & 1,51 & 280 \\ \hline \mathrm{~V}(\mathrm{~mL}) & 50 & 200 & 100 & 0,43 & 400 \\ \hline \rho(\mathrm{~g} / \mathrm{mL}) & & & & & \\ \hline \end{array}$
Exercice 3:
La masse volumique de l’eau est de $1 g/mL$, ce qui veut dire que chaque volume d’un millilitre ($1 \mathrm{~mL}$) d’eau a une masse d’un gramme ($1 \mathrm{~g}$). Tu sais qu’un litre ($1 \mathrm{~L}$) équivaut à $1000 \mathrm{~mL}$. Détermine alors quelle est la masse d’un litre d’eau.
On a : $\quad \rho=\frac{m}{V}$
Alors: $m=V \times \rho$
et On a : $V=1 L=1000 \mathrm{~mL}$
Alors : $m=1000 \times 1$
Donc : $m=1000 \mathrm{~g}=1\mathrm{~Kg}$
Exercice 4:
Un objet en Aluminium a pour masse $700\mathrm{~g}$.Quel est son volume ?
(Avec $\rho=2,7 \mathrm{~g} / \mathrm{cm}^{3}$ pour l’aluminium).
Exercice 5:
Soit la masse $m=24 g$ d’huile occupant un volume $V=30 \mathrm{~cm}^{3}$.
$1)$ Calculer la masse volumique d’huile.
$2)$ Quelle sera la masse d’un litre d’huile ?
$3)$ Quel volume occupera $\mathbf{5 0 0 g}$ d’huile ?
Exercice 6:
Compléter le tableau suivant :
$\begin{array} {|r|r|}\hline Corps & A & B & C \\ \hline Masse (\mathrm{g}) & 320 & m_{B} & 420 \\ \hline Volume (\mathrm{l}) & 64 & 60 & V_{C} \\ \hline \rho(g / l) & \rho_{A} & 7.8 & 2.7 \\ \hline \end{array}$
Exercice 7:
On a mesuré la masse d’un même volume $\boldsymbol{V}=\mathbf{2 0 0} \boldsymbol{m} \boldsymbol{L}$ de trois corps différents $A, B$ et $C$.
On a trouvé les masses suivantes : $\boldsymbol{m}_{A}=\mathbf{2 0 0} \boldsymbol{g}$; $\boldsymbol{m}_{B}=\mathbf{1 6 0} \boldsymbol{g}$ et $\boldsymbol{m}_{C}=\mathbf{5 4 0 ~ m g}$.
$1)$ Calculer la masse volumique des trois corps $A$, $B$ et $C$.
$2)$ Classer ces corps en donnant lequel va flotter sur l’autre. Justifier votre réponse
Exercice 8:
Ahmed a trouvé un morceau de métal. Pour savoir sa nature, il réalise l’expérience suivante :
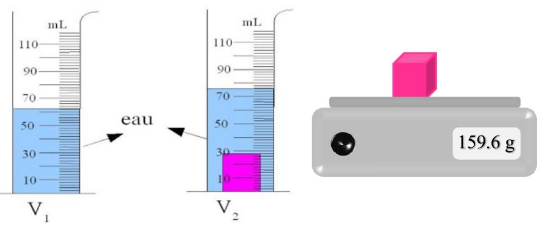
$1)$ Quelle est le volume de ce métal ?
$2)$ Quelle est sa masse ?
$3)$ Identifier la nature de ce métal. On donne :
$\begin{array} {|r|r|}\hline Métal & Fer & Aluminium & Cuivre & Plomb \\ \hline \rho\left(\mathrm{g} / \mathrm{cm}^{2}\right) & 7.8 & 2.7 & 8.9 & 11.4 \\ \hline \end{array}$
Exercice 9:
On place sur une balance électronique une Eprouvette graduée vide, on verse une quantité d’huile. (Figure 1 et 2)

$1)$ Calculer la masse d’huile.
$2)$ Calculer le volume d’huile dans l’éprouvette graduée.
$3)$ Calculer la masse volumique de l’huile.
$4)$ L’huile est-elle plus lourde ou plus légère que l’eau ? justifier.
La masse volumique exercices corrigés
