Théorème de Pythagore exercices corrigés 3AC
Exercice 1:
$DEF$ est un triangle rectangle en $D$ tel que : $DE = 15 cm \quad et \quad DF = 8 cm.$
Calculer $EF.$
On sait que ……. est un triangle rectangle en ……
D’après le théorème de Pythagore :
1. $\quad \ldots \ldots^{2} = \ldots \ldots^{2}+\ldots \ldots^{2}$
2. $\quad \ldots \ldots^{2} = \ldots \ldots^{2}+\ldots \ldots^{2}$
3. $\quad \ldots \ldots^{2} = \ldots +\ldots $
$\ldots \ldots^{2}=\ldots $
4. $\quad \ldots \ldots=\sqrt{\ldots \ldots}=\ldots \ldots \mathrm{cm}$
$DEF$ est un triangle rectangle en $D$ tel que :
$DE = 15 cm \quad et \quad DF = 8 cm.$
Calculer $EF.$
On sait que $DEF$ est un triangle rectangle en $D$
D’après le théorème de Pythagore :
1. $\quad EF^{2} = DE^{2}+DF^{2}$
2. $\quad EF^{2} = 15^{2}+8^{2}$
3. $\quad EF^{2} = 225 +64 $
$EF^{2}=289 $
4. $\quad EF=\sqrt{289}=17\mathrm{cm}$
Exercice 2:
$DEF$ est un triangle rectangle en $D$ tel que : $DE = 48 cm \quad et \quad EF = 52 cm.$
Calculer $DF.$
On sait que ……. est un triangle rectangle en ……
D’après le théorème de Pythagore :
1. $\quad \ldots \ldots^{2}+\ldots \ldots^{2}=\ldots \ldots^{2}$
2. $\quad \ldots \ldots^{2}+\ldots \ldots^{2}=\ldots \ldots^{2}$
3. $\quad \ldots +\ldots \ldots^{2}=\ldots $
4. $\quad \ldots \ldots^{2}=\ldots -\ldots $
$\ldots \ldots^{2}=\ldots $
5. $\quad \ldots \ldots=\sqrt{\ldots \ldots}=\ldots \ldots \mathrm{cm}$
$DEF$ est un triangle rectangle en $D$ tel que :
$DE = 48 cm \quad et \quad EF = 52 cm.$
Calculer $DF.$
On sait que $DEF$ est un triangle rectangle en $D$
D’après le théorème de Pythagore :
1. $\quad DE^{2}+DF^{2}=EF^{2}$
2. $\quad 48^{2}+DF^{2}=52^{2}$
3. $\quad 2304 +\ldots \ldots^{2}=2704 $
4. $\quad DF^{2}=2704 -2304 $
$DF^{2}=400 $
5. $\quad DF=\sqrt{400}=20 \mathrm{cm}$
Exercice 3:
$A B C$ est un triangle rectangle en $A$ tel que :
$A B=12 \mathrm{~cm}$
$A C=16 \mathrm{~cm}$
Calculer la longueur $BC$.
$ABC$ est un triangle rectangle en $A$ donc d’après le théorème de Pythagore :
$\mathrm{BC}^{2}=\mathrm{AB}^{2}+\mathrm{AC}^{2}=12^{2}+16^{2}=144+256=400$
$\mathrm{BC}=\sqrt{400}=20 \mathrm{~cm}$
Exercice 4:
LMN est un triangle rectangle en $L$ tel que :
$\mathrm{LM}=6,8 \mathrm{~cm}$
$M N=6,89 \mathrm{~cm}$
Calculer la longueur $LN$.
$LMN$ est un triangle rectangle en $L$ donc d’après le théorème de Pythagore :
$\mathrm{MN}^{2}=\mathrm{LM}^{2}+\mathrm{LN}^{2}$
$\Leftrightarrow 6,89^{2}=6,8^{2}+\mathrm{LN}^{2} $
$\Leftrightarrow 6,89^{2}-6,8^{2}=\mathrm{LN}^{2} $
$\Leftrightarrow 1,2321=\mathrm{LN}^{2} $
$ \Leftrightarrow \mathrm{LN}=\sqrt{1,2321}=1,11$
Exercice 5:
$DEF$ est un triangle tel que : $DE = 15 cm$ , $DF = 12 cm$ et $EF = 9 cm$
Ce triangle est-il rectangle ?
1. Le grand côté est $[ \ldots]$
$\ldots^{2}= \ldots^{2} = \ldots$
2. $\quad \ldots \ldots^{2}+\ldots \ldots^{2}=\ldots \ldots^{2} + \ldots \ldots^{2}$
$\quad =\ldots + \ldots $
$\quad = \ldots $
3. Ainsi : $\quad \ldots \ldots^{2}=\ldots \ldots^{2}+\ldots \ldots^{2} $
D’après la réciproque du théorème de Pythagore, le triangle $DEF$ est rectangle en $F$.
1. Le grand côté est $[ DE]$
$DE^{2}= 15^{2} = 225$
2. $\quad DF^{2}+EF^{2}=12^{2} + 9^{2}$
$\quad =144 + 81 $
$\quad = 225 $
3. Ainsi : $\quad DE^{2}=DF^{2}+EF^{2} $
D’après la réciproque du théorème de Pythagore, le triangle $DEF$ est rectangle en $F$.
Exercice 6:
$A B C$ est un triangle tel que : $A B=4,5 \mathrm{~cm} \quad A C=2,7 \mathrm{~cm} \quad B C=3,6 \mathrm{~cm}$
Démontrer que $A B C$ est un triangle rectangle.
$A B=4,5 \mathrm{~cm} ; A C=2,7 \mathrm{~cm} ; B C=3,6 \mathrm{~cm}$
Le plus grand côté est $[A B]: \mathrm{AB}^{2}=4,5^{2}=20,25$
$\mathrm{AC}^{2}+\mathrm{BC}^{2}=2,7^{2}+3,6^{2}=7,29+12,96=20,25$
Ainsi : $\mathrm{AB}^{2}=\mathrm{AC}^{2}+\mathrm{BC}^{2}$
D’après la réciproque du théorème de Pythagore : le triangle $ABC$ est rectangle en $C$.
Exercice 7:
DEF est un triangle tel que : $D E=15,3 \mathrm{~cm} \quad D F=10,7 \mathrm{~cm} \quad E F=18,2 \mathrm{~cm}$
Ce triangle est-il rectangle ?
$\mathrm{DE}=15,3 \mathrm{~cm} ; \mathrm{DF}=10,7 \mathrm{~cm} ; \mathrm{EF}=18,2 \mathrm{~cm}$
Le plus grand côté est [EF] : $\mathrm{EF}^{2}=18,2^{2}=331,24$
$\mathrm{DE}^{2}+\mathrm{DF}^{2}=15,3^{2}+10,7^{2}=234,09+114,49=348,58$
Ainsi : $\mathrm{EF}^{2} \neq \mathrm{DE}^{2}+\mathrm{DF}^{2}$
La réciproque du théorème de Pythagore ne s’applique pas: le triangle $DEF$ n’est pas rectangle.
Exercice 8:
$(A H)$ est la hauteur du triangle $A B C$ issue de $A$.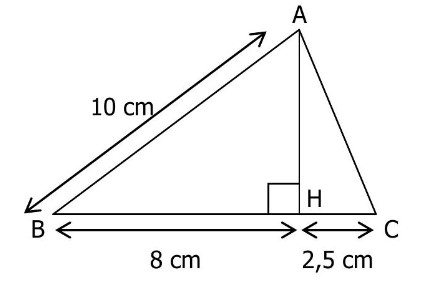
a. Calculer la longueur AH.
b. En déduire la longueur $A C$.
c. Le triangle $A B C$ est-il rectangle ?
a. ABH est un triangle rectangle en H donc d’après le théorème de Pythagore :
$ \mathrm{AB}^{2}=\mathrm{AH}^{2}+\mathrm{BH}^{2} $
$\Leftrightarrow 10^{2}=\mathrm{AH}^{2}+8^{2} $
$ \Leftrightarrow \mathrm{AH}^{2}=10^{2}-8^{2}=36 $
$\Leftrightarrow \mathrm{AH}=\sqrt{36}=6$
b. En déduire la longueur $A C$.
ACH est un triangle rectangle en H donc d’après le théorème de Pythagore :
$\mathrm{AC}^{2}=\mathrm{AH}^{2}+\mathrm{CH}^{2}=6^{2}+2,5^{2}=42,25$
$A C=\sqrt{42,25}=6,5$
c. Le triangle $A B C$ est-il rectangle
Le plus grand côté est [BC]:
$B C=8+2,5=10,5 \mathrm{~cm}$
$\rightarrow \mathrm{BC}^{2}=10,5^{2}=110,25$
$\mathrm{AB}^{2}+\mathrm{AC}^{2}=10^{2}+6,5^{2}=100+42,25=142,25$
Ainsi: $\mathrm{BC}^{2} \neq \mathrm{AB}^{2}+\mathrm{AC}^{2}$
La réciproque du théorème de Pythagore ne s’applique pas: le triangle $A B C$ n’est pas rectangle.
Exercice 9:
$A B C D$ est un losange de centre $O$ avec $A C=20 \mathrm{~cm}$ et $B D=48 \mathrm{~cm}$.
a. Faire une figure à main levée.
b. Calculer AB
c. Calculer le périmètre de ce losange.
a. Faire une figure à main levée.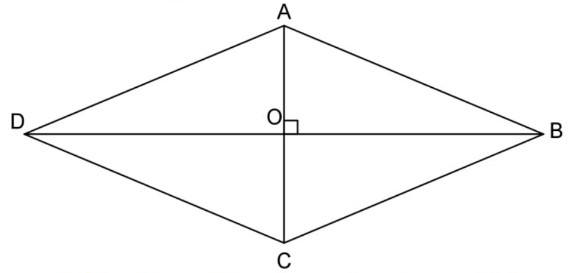
b. ABO est un triangle rectangle en $\mathbf{O}$ donc d’après le théorème de Pythagore :
$\mathrm{AB}^{2}=\mathrm{AO}^{2}+\mathrm{BO}^{2}=10^{2}+24^{2}=676 $
$\mathrm{AB}=\sqrt{676} \simeq 26 \mathrm{~cm}$
c. Les côtés d’un losange sont tous de même longueur, donc le périmètre mesure :
$p=4 \times \mathrm{AB}=4 \times 26=104 \mathrm{~cm}$
Exercice 10:
ABCDEFGH est un pavé droit de longueur 4 cm , de largeur 3 cm et de hauteur 12 cm .
Calculer la longueur EG puis la diagonale AG.
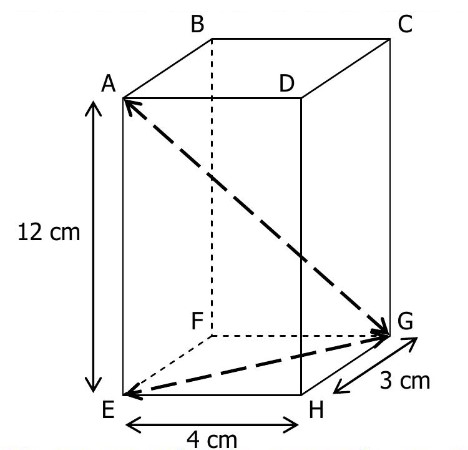
EFG est un triangle rectangle en $F$ donc d’après le théorème de Pythagore :
$\mathrm{EG}^{2}=\mathrm{EF}^{2}+\mathrm{FG}^{2}=3^{2}+4^{2}=25 $
$\mathrm{EG}=\sqrt{25}=5 \mathrm{~cm}$
AEG est un triangle rectangle en $E$ donc d’après le théorème de Pythagore :
$\mathrm{AG}^{2}=\mathrm{AE}^{2}+\mathrm{EG}^{2}=12^{2}+25=169$
$\mathrm{AG}=\sqrt{169}=13 \mathrm{~cm}$
Exercice 11:
(OC) est la hauteur du triangle BCD issue de C.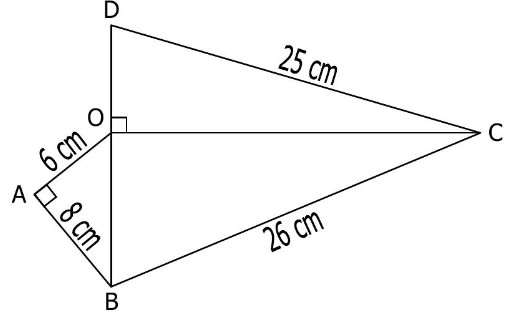
Le but de l’exercice est de déterminer l’aire du triangle BCD.
1. a. Calculer la longueur $O B$.
b. Calculer la longueur OC.
c. Calculer la longueur OD.
2. En utilisant les résultats du 1., calculer l’aire du triangle BCD.
On rappelle la formule : $\quad$ Aire $=(b \times h) / 2$
1. a. Calculer la longueur $O B$.
OAB est un triangle rectangle en $A$ donc d’après le théorème de Pythagore :
$\mathrm{OB}^{2}=\mathrm{OA}^{2}+\mathrm{AB}^{2}=6^{2}+8^{2}=100$
$\mathrm{OB}=\sqrt{100}=10 \mathrm{~cm}$
b. Calculer la longueur OC.
OBC est un triangle rectangle en $O$ donc d’après le théorème de Pythagore :
$\mathrm{BC}^{2}=\mathrm{BO}^{2}+\mathrm{CO}^{2} \Leftrightarrow 26^{2}=10^{2}+\mathrm{CO}^{2}$
$\Leftrightarrow 26^{2}-10^{2}=\mathrm{CO}^{2} \Leftrightarrow \mathrm{CO}^{2}=576$
$\mathrm{CO}=\sqrt{576}=24 \mathrm{~cm}$
c. Calculer la longueur OD.
OCD est un triangle rectangle en $O$ donc d’après le théorème de Pythagore :
$ \mathrm{CD}^{2}=\mathrm{CO}^{2}+\mathrm{DO}^{2} \Leftrightarrow 25^{2}=24^{2}+\mathrm{DO}^{2}$
$ \Leftrightarrow 25^{2}-24^{2}=\mathrm{DO}^{2} \Leftrightarrow \mathrm{DO}^{2}=49 $
$ \mathrm{DO}=\sqrt{49}=7 \mathrm{~cm}$
2. L’aire du triangle $B C D$ est :
$\frac{\mathrm{BD} \times \mathrm{CO}}{2}=\frac{(10+7) \times 24}{2}=17 \times 12=204 \mathrm{~cm}^{2}$
Exercice 12:
ABC est un triangle rectangle en A.
(AH) est la hauteur issue du sommet de l’angle droit.
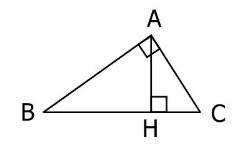
1. a. Exprimer l’aire de ce triangle en fonction de $A B$ et $A C$.
b. Exprimer l’aire de ce triangle en fonction de $A H$ et $BC$ .
c. En déduire une égalité faisant intervenir $A B$, $A C, B C$ et $A H$.
2. Calculer la hauteur $A H$ pour le triangle $A B C$ rectangle en A :
$A B=4 \mathrm{~cm} \quad A C=3 \mathrm{~cm} \quad B C=5 \mathrm{~cm}$
1. a. L’aire du triangle $A B C$ est : $\frac{A B \times A C}{2}$
b. L’aire du triangle $A B C$ est : $\frac{\mathrm{BC} \times \mathrm{AH}}{2}$
c. D’après les questions a. et b. : $\frac{\mathrm{AB} \times \mathrm{AC}}{2}=\frac{\mathrm{BC} \times \mathrm{AH}}{2}$
2. $\frac{\mathrm{AB} \times \mathrm{AC}}{2}=\frac{\mathrm{BC} \times \mathrm{AH}}{2} \Leftrightarrow \frac{4 \times 3}{2}=\frac{5 \times \mathrm{AH}}{2}$
$\Leftrightarrow 6=\frac{5 \times \mathrm{AH}}{2} \Leftrightarrow 12=5 \times \mathrm{AH}$
$\Leftrightarrow \mathrm{AH}=\frac{12}{5}=2,4 \mathrm{~cm}$
Exercice 13:
On construira la figure. On écrira le raisonnement pour chaque réponse $A B C D$ est un rectangle de côtés $A B=12 \mathrm{~cm}$ et $A D=9 \mathrm{~cm}$. Sur le côté [BC] on place le point E tel que $A E=13 \mathrm{~cm}$. Sur le côté [DC] on place le point F tel que $D F=5 \mathrm{~cm}$.
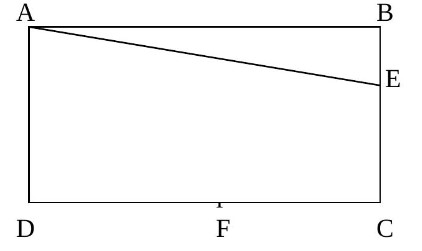
1) Calculer la longueur AF.
2) Calculer la longueur BE.
3) Calculer les longueurs CE et CF, puis la longueur EF.
4) Le triangle AFE est-il rectangle ?
ABCD est un rectangle, donc ses angles sont droits.
1) Le triangle $A D F$ est rectangle en $D$, d’après le théorème de Pythagore :
$A F^{2}=A D^{2}+D F^{2} $
$ A F^{2}=9^{2}+5^{2} $
$A F^{2}=81+25 $
$A F^{2}=106 $
$A F=\sqrt{106} \mathrm{~cm}$
2) Le triangle $A B E$ est rectangle en $B$, d’après le théorème de Pythagore :
$ A E^{2}=A B^{2}+B E^{2} $
$13^{2}=12^{2}+B E^{2} $
$169=144+B E^{2} $
$169-144=B E^{2} $
$ B E^{2}=25 $
$ B E=5 \mathrm{~cm}$
3) $\mathrm{E} \in[\mathrm{BC}]$ donc $C E=B C-E B=9-5=4 \mathrm{~cm}$
$\mathrm{F} \in[\mathrm{CD}]$ donc $C F=C D-D F=12-5=7 \mathrm{~cm}$
Le triangle ECF est rectangle en $C$; d’après le théorème de Pythagore :
$ E F^{2}=E C^{2}+C F^{2} $
$E F^{2}=4^{2}+7^{2} $
$E F^{2}=16+49=65 $
$ E F=\sqrt{65} \mathrm{~cm}$
4) Dans le triangle $A E F, A E$ est le plus grand côté,
$A E^{2}=13^{2}=169$
$A F^{2}+E F^{2}=106+65=171 \quad \text { (il faut prendre les valeurs exactes de } A F^{2} \text { et } E F^{2} \text { ) }$
donc $A E^{2} \neq A F^{2}+E F^{2}$
La réciproque du théorème de Pythagore ne s’applique pas, le triangle AEF n’est pas rectangle.
Exercice 14:
1) Construire le triangle ABC tel que $\mathrm{CB}=169 \mathrm{~mm}, \mathrm{AB}=65 \mathrm{~mm}$ et $\mathrm{AC}=156 \mathrm{~mm}$.
2) Démontrer que le triangle $A B C$ est rectangle en $A$.
3) Calculer l’aire du triangle $A B C$.
4) Tracer la hauteur $A H$ du triangle $A B C$.
$\rightarrow$ En utilisant une autre expression qu’en 2) de l’aire de ABC , calculer simplement AH .
1) Utiliser le compas, garder le mm comme unité. (on ignore que le triangle est rectangle, donc on n’utilise ni équerre, ni demi cercle).
2) Le plus grand côté est $B C$. On calcule :
$ B C^{2}=169^{2}=28561 $
$ B A^{2}+A C^{2}=65^{2}+156^{2}=4225+24336=28561$
Ainsi : $B C^{2}=B A^{2}+A C^{2}$
D’après la réciproque de l’énoncé de Pythagore, le triangle ABC est rectangle en A .
3) L’aire d’un triangle est : Aire $=\frac{\text { base } \times \text { hauteur }}{2}$
$\text { Aire }_{A B C} =\frac{A B \times A C}{2} $
$ =\frac{65 \times 156}{2} $
$ =5070 \mathrm{~mm}^{2}$
4) On utilise les deux formules de calcul d’aire dans un triangle rectangle, cette fois-ci avec l’hypoténuse :
$ \text { Aire }=\frac{\text { base } \times \text { hauteur }}{2}$
$ \text { Aire }_{A B C}=\frac{B C \times A H}{2} $
$5070=\frac{169 \times A H}{2} $
$ 5070 \times 2=169 \times A H $
$ A H=\frac{5070 \times 2}{169}=60 \mathrm{~mm}$
Théorème de Pythagore exercices corrigés 3AC
