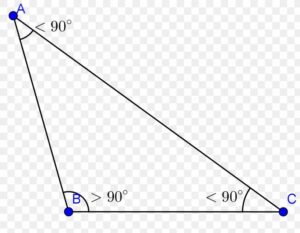
Les triangles, formes géométriques fondamentales, offrent une riche variété de propriétés et d’applications. Parmi eux, le triangle obtusangle, caractérisé par la présence d’un angle obtus, suscite l’intérêt tant dans le domaine de la géométrie .
Dans cet article, nous explorerons les définitions, propriétés et applications du triangle obtusangle.
I. Définition du Triangle Obtusangle
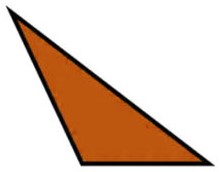
Un triangle obtusangle est défini par la présence d’au moins un angle obtus, c’est-à-dire un angle mesurant plus de 90 degrés. Contrairement au triangle acutangle, où tous les angles sont aigus.
le triangle obtusangle présente un angle qui s’étend au-delà de la mesure standard de 90 degrés. La somme totale des angles d’un triangle reste, bien entendu, égale à 180 degrés.
II. Propriétés Distinctives
a. Angle Obtus :
La caractéristique principale du triangle obtusangle est la présence d’au moins un angle obtus. Cela confère au triangle une asymétrie visuelle, les autres angles étant aigus.
b. Côtés Variés :
Les côtés du triangle peuvent varier en longueur, tout comme dans d’autres types de triangles. Cette variabilité offre une flexibilité dans l’application de ce triangle dans divers contextes.
III. Applications Pratiques
a. Ingénierie et Architecture :
Dans le domaine de l’ingénierie et de l’architecture, les triangles obtusangles sont souvent utilisés pour modéliser des formes et résoudre des problèmes impliquant des angles non standard.
b. Géodésie :
En géodésie, la science de la mesure de la forme et de la taille de la Terre, les triangles obtusangles peuvent être utilisés pour calculer des distances et des angles difficiles à mesurer autrement.
c. Navigation :
La navigation maritime utilise également des triangles obtusangles dans des calculs liés aux angles de visée et aux trajets à travers des voies d’eau complexes.
Conclusion :
Une perspective angulaire le triangle obtusangle, avec son angle non conventionnel, offre une perspective angulaire intéressante dans le monde de la géométrie.
Ses propriétés uniques trouvent des applications pratiques dans divers domaines, de l’ingénierie à la navigation.
Comprendre la nature de ce triangle enrichit notre compréhension des formes géométriques et souligne son importance dans des contextes réels.
En somme, ce triangle nous rappelle que la géométrie va au-delà des formules, influençant notre compréhension et notre interaction avec le monde qui nous entoure.