Inégalité triangulaire et médiatrice 1AC exercices corrigés
Exercice 1:
Dans chaque cas, dire s’il est possible de construire un triangle $A B C$.
1. $A B=9 \mathrm{~cm}, B C=5 \mathrm{~cm}, A C=1 \mathrm{~cm}$.
2. $A B=6,5 \mathrm{~cm}, B C=7 \mathrm{~cm}, A C=5 \mathrm{~cm}$.
3. $A B=3,7 \mathrm{~cm}, B C=2,3 \mathrm{~cm}, A C=6 \mathrm{~cm}$.
1. $B C+A C=5 \mathrm{~cm}+1 \mathrm{~cm}=6 \mathrm{~cm}$
$A B=9 \mathrm{~cm}$
Donc $B C+A C<A B$. On ne peut pas construire le triangle.
2. $A B+A C=6,5 \mathrm{~cm}+5 \mathrm{~cm}=11,5 \mathrm{~cm}$
$B C=7 \mathrm{~cm}$
Donc $A B+A C>B C$. On peut construire le triangle $A B C$.
3. $A B+B C=3,7 \mathrm{~cm}+2,3 \mathrm{~cm}=6 \mathrm{~cm}$
$A C=6 \mathrm{~cm}$
Donc $A B+B C=A C$. Les points $A, B$ et $C$ sont alignés.
Exercice 2:
1. Tracer un segment $[A B]$ de longueur 8 cm .
2. Lire ce dialogue. Qui a raison? Expliquer.

Exercice 3:
Ali souhaite construire un enclos triangulaire dont un côté mesure $8 m$ . Pour cela, il achète $15 m$ de fil de fer. Que peut-on en penser?
Exercice 4:
Tracer un triangle ABC tel que
$AB = 11 cm\quad$ $\quad EG = 8 cm\quad$ et $\quad FG = 6 cm$
Tracer les médiatrices des côtés du triangle.
Exercice 5:
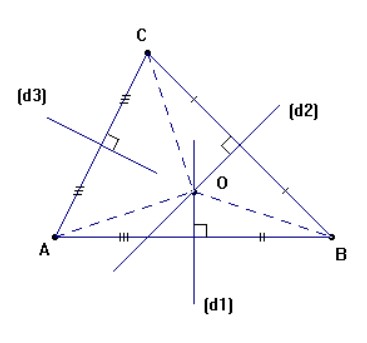
$ABC$ est un triangle
$(d1)$ est la médiatrice de $ [AB]$
$(d2) $ est la médiatrice de $ [BC]$
Les deux médiatrices $(d1)$ et $(d2)$ se coupent en $ O$.
$(d3)$ est la médiatrice de $[AC]$
1) Démontrer que le point $O$ appartient aussi à $(d3)$
2) Recopier et compléter la propriété suivante (importante à retenir)
Les trois médiatrices d’un triangle sont …
Le point de concours des trois médiatrices est le … d’un cercle qui passe par les … du triangle.
Ce cercle est appelé …..au triangle.
Exercice 6:
$ABC$ et un triangle tels que $BC = 7 cm, AC = 4 cm et AB = 6 cm$
La médiatrice $(Δ )$ de $[BC]$ coupe la droite $(AB)$ en $M$.
Soit le point $N$ le projeté orthogonal de point A sur la droite $(BC)$
1) Faire une figure.
2) Montrer que $MBC$ est un triangle Isocèle.
3) Calculer $AM+MC$
4) Montrer que $(Δ ) // (AN)$
Exercice 7:
1) Tracer un cercle $(C)$ de centre $O$ et de Rayon $4 cm$.
– Placer deux point $A$ et $B$ sur le cercle $(C)$ tel que $AB = 6 cm$
– Tracer la corde $[AB]$
– Placer le point $M$ milieu de $ [AB]$
2) Montrer que $(OM)$ est La médiatrice du segment $[AB]$ ?
Exercice 8:
Tracer un cercle $(C)$ de centre $O$ et de Rayon $4 cm$.
Soit $[BP]$ un diamètre de $(C)$.
La médiatrice de $[OB]$ coupe $[OB]$ en $N$ et le cercle $(C)$ en $E$ et $F$.
$(Δ)$ est la médiatrice de $[ON]$ coupe $[ON]$ en $I$.
1) Faire une figure.
2) Montrer que $(Δ ) // (EF)$
3) Calculer $BI$
4) Montrer que $PE = PF$
