Puissances exercices corrigés 3AC

Cours
Évaluations corrigés
Exercices corrigés

• Puissances de 10

Exercice 1: 

Calculer mentalement :

Exercice 2: 

Calculer mentalement :

Exercice 3: 

Écrire chaque résultat sous la forme « 10ª » :

Exercice 4: 

Écrire chaque résultat sous la forme « 10ª » :

Exercice 5: 

Écrire chaque résultat sous la forme « 10ª » :

Exercice 6: 

Compléter les pointillés :

 

Exercice 7: 

Calculer :

Exercice 8: 

Compléter les pointillés :

• Puissances entières d’un nombre relatif

Exercice 9: 

Calculer :

Exercice 10: 

Calculer :

Exercice 11: 

Donner le résultat des calculs suivants sous la forme « nª » :

• Opérations et priorité des calculs

Exercice 12: 

Calculer en respectant les priorités :

Exercice 13: 

Calculer en respectant les priorités :

Exercice 14: 

Calculer mentalement en utilisant astucieusement la
« distributivité des puissances » :

Exercice 15: 

Calculer mentalement en utilisant astucieusement la
« distributivité des puissances » :

• Notation scientifique

Exercice 16: 

Parmi les nombres suivants, entourer ceux qui sont en écriture scientifique :

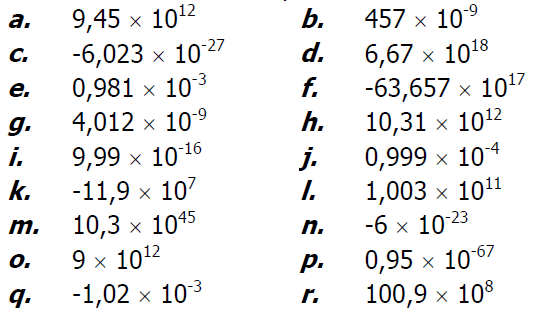
Exercice 17: 

Compléter le tableau :

 

Exercice 18: 

Retrouver la bonne écriture scientifique :

Exercice 19: 

1- Compléter le tableau :

2- Compléter le tableau :

1- Compléter le tableau :

2- Compléter le tableau :

Exercice 20: 

1- Comparer ces nombres en écriture scientifique :

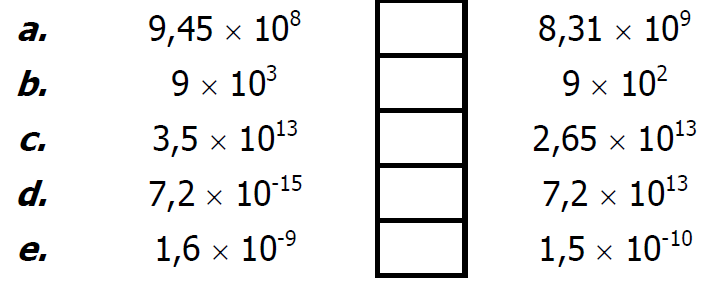
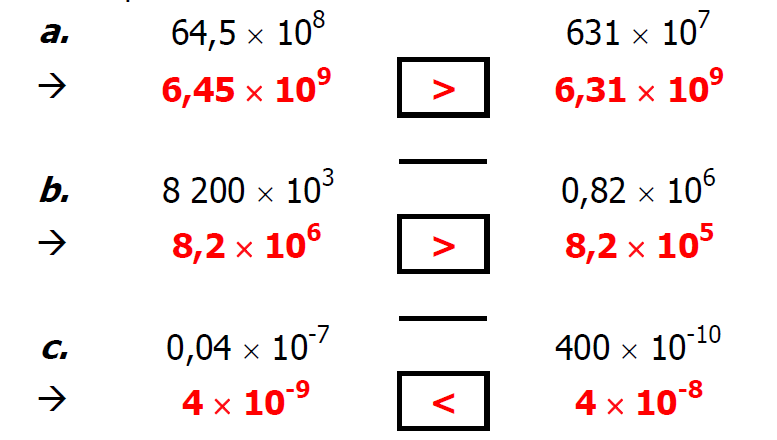
2- Donner l’écriture scientifique des deux nombres puis les comparer :

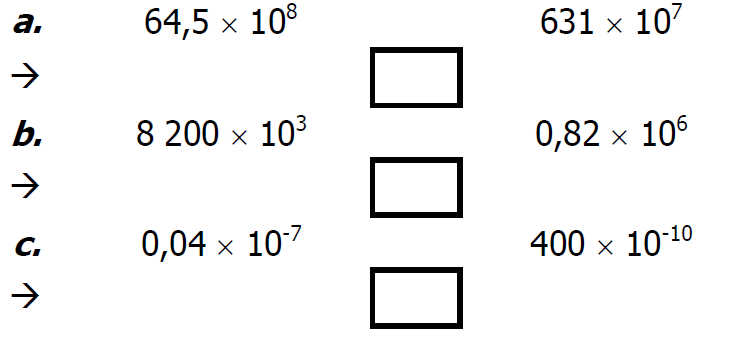
1- Comparer ces nombres en écriture scientifique :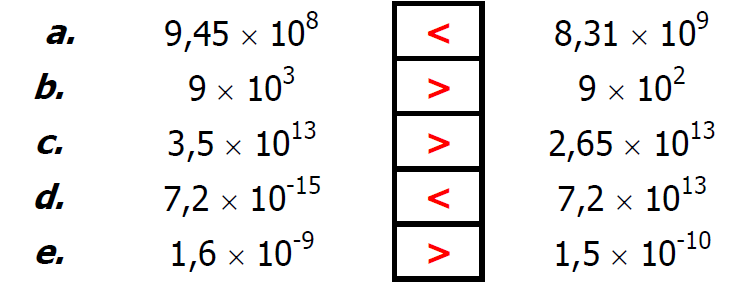

2- Donner l’écriture scientifique des deux nombres puis les comparer :

Exercice 21: 

Exercice 22: 

Puissances exercices corrigés 3AC