Symétrie axiale exercices corrigés 2AC
Exercice 1:
$1)$ Rappel de la définition de la symétrie axiale: (compléter la phrase suivante)
Deux points $A$ et $B$ sont symétriques par rapport à la droite $(d)$$……$
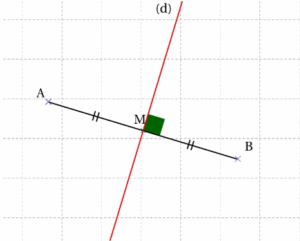
$2)$-$a)$ Sur papier uni, tracer un segment $[A B]$ de longueur $5 cm$ . Placer son milieu $M$.
$b)$ Tracer en rouge la médiatrice $(d)$ du segment $[A B]$.
$1)$ Deux points $A$ et $B$ sont symétriques par rapport à la droite $(d)$ si $(d)$ est la médiatrice du segment $[A B]$
$a)$ et $b)$
Exercice 2:
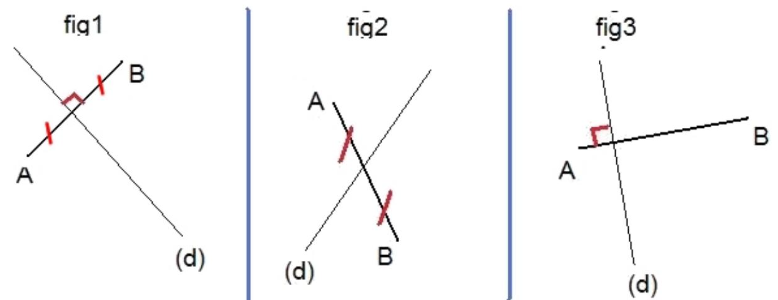
Dans chaque cas, dire sir le point $B$ est le symétrique du point $A$ par rapport à la droite $(d)$ en justifiant la réponse.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 3:
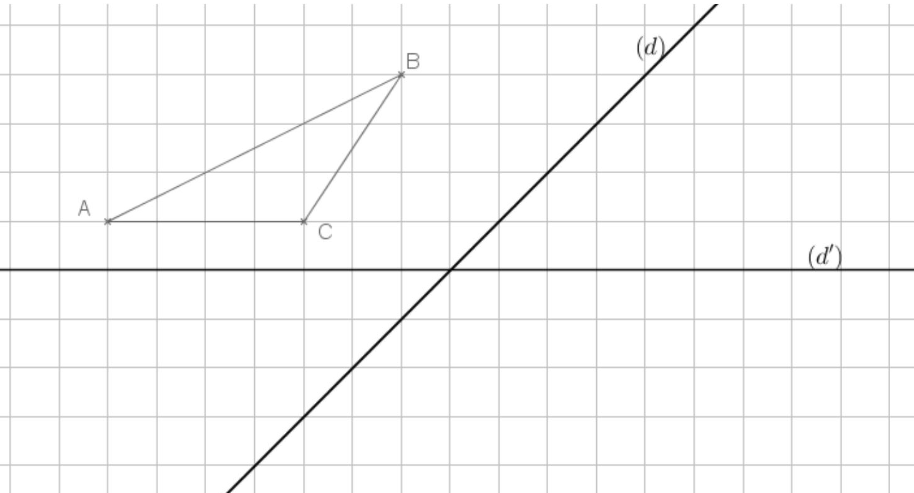
Construire le symétrique(en rouge) du triangle $A B C$ par rapport à (d) puis le symétrique du triangle $A B C$ par rapport à $\left(d^{\prime}\right)$ en utilisant le quadrillage.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 4: Constructions au compas
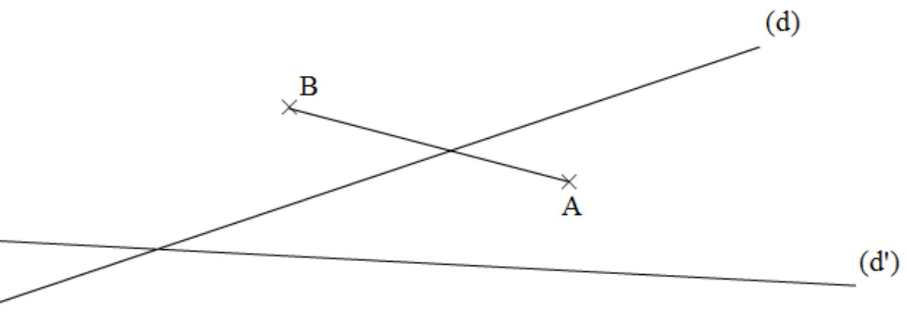
$1)$ Construire le symétrique $\left[A^{\prime} B^{\prime}\right]$ du segment $[A B]$ avec au compas par rapport à $(d)$.
$2)$ Construire le symétrique $\left(d_{1}\right)$ de la droite $\left(d^{\prime}\right)$ par rapport à $(d)$ à la règle et au compas.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 5: Symétrique d’un cercle
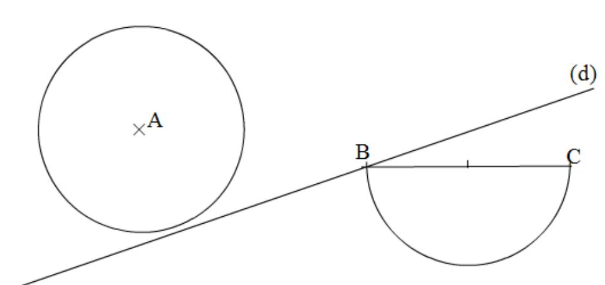
$1)$ Construire le symétrique du cercle de centre $A$ par rapport à ( $d$ ).
$2)$ Construire le symétrique du demi-cercle de diamètre $[B C]$ par rapport à $(d)$.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 6:
$1)$ Sur la figure ci-dessous le point $ A^{\prime}$ est le symétrique de $A$ par rapport à une droite qui a été effacée.
• Retrouver graphiquement cette droite en expliquant le pourquoi de votre construction.
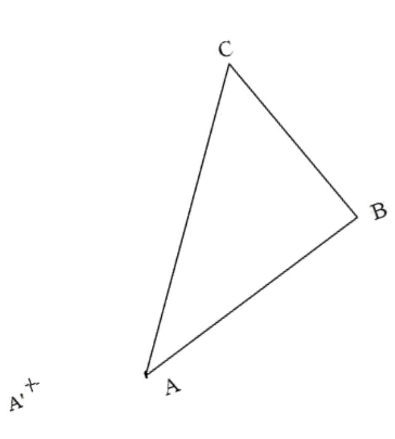
$2)$ Tracer alors le symétrique $A^{\prime} B^{\prime} C^{\prime}$ du triangle $A B C$ par rapport à $(d)$.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 7:
On donne la figure ci-dessous :
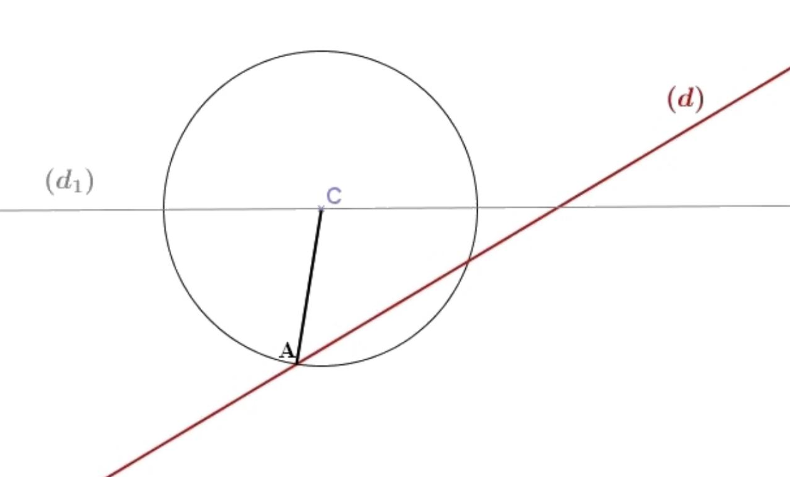
$1)$ Quel est le symétrique du point $A$ par rapport à $(d)$ ?
$2)$ Construire le symétrique du cercle de centre $C$ et de rayon $[C A]$ par rapport à $(d)$.
$3)$ Construire le symétrique $\left(d_{1}^{\prime}\right)$ de la droite $\left(d_{1}\right)$ par rapport à $(d)$.
$4)$ Quel est le symétrique du cercle de centre $C$ et rayon $[C A]$ par rapport à $\left(d_{1}\right)$ ?
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 8:
$1)$ Construire un triangle $L M P$ isocèle en $P$ tel que $L M=6 \mathrm{~cm}$ et $L P=4 \mathrm{~cm}$.
$2)$ Construire au compas l’image de ce triangle par rapport à $(L M)$. On appelle $N$ le symétrique de $P$.
$3)$ Quelle est la nature du quadrilatère $L P M N$ ainsi formé? Justifier la réponse.
$4)$ Les points $L$ et $M$ sont-ils symétriques? Si oui, par rapport à quelle droite ? Justifier.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 9:
$1)$ Tracer deux cercles de même rayon qui se coupent en $M$ et en $N$.
$2)$ Tracer le segment qui joint les centres $A$ et $B$ de ces deux cercles.
$3)$ Tracer la droite $(MN)$.
$4)$ Que semble représenter la droite $(MN)$ pour le segment $[AB]$?
$5)$ Que semble représenter la droite $(AB)$ pour le segment $[MN]$?
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 10:
$1)$ Tracer un segment $[AB]$ puis sa médiatrice $(d)$.
$2)$ Quel est le symétrique de $A$ par rapport à $(d)$?
$3)$ Quel est le symétrique de $B$ par rapport à $(d)$?
$4)$ Placer un point $K$ sur $(d)$ et n’appartenant pas à $[AB]$. Quel est le symétrique de $K$ par rapport à $(d)$?
$5)$ Que peut-on dire des longueurs $KA$ et $KB$ ?
$6)$ Que peut-on dire du triangle $BAK$?
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 11:
On considère le triangle $ABC$ tel que $AB = 4,5 cm, AC = 6 cm$ et $BC = 4 cm$. et $(d)$ une droite quelconque :
$1)$ Construire ce triangle.
$2)$ Tracer les symétriques $A’ ,B’$ et $C’$ de $A ,B$ et $C$ par rapport à $(d)$.
$3)$ Construire le triangle $A’B’C’$.
$4)$ Que peut-on dire des segments $[AC]$ et $[A’C’]$ ? Justifier.
$5)$ Quel angle a la même mesure que l’angle $BÂC$ ? Justifier.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 12 :
$ABC$ est un triangle rectangle en A tel que : $AB= 5 cm$ et $\widehat{ABC}=50°$
Soit $B’$ le symétrique de $B$ par rapport à $A$.
$1)$ Faire une figure
$2)$ Montrer que $B’$ est le symétrique de $B$ par rapport à $(AC)$.
$3)$ En déduire la mesure de l’angle $CB’B$
$4)$ Soit $D$ un point de $BC (D≠ B et D ≠ C)$.
• Construire $D’$ le symétrique de $D$ par rapport à la droite $(AC)$
$5)$Montrer que : $BD=B’D’$
$6)$ Montrer que les points $D’, B’$ et $C$ sont alignés.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Symétrie axiale exercices corrigés 2AC
