Théorème de Pythagore – Évaluations corrigés

Évaluation de Mathématiques

Théorème de Pythagore

Matière :Mathématiques

Niveau :3^ème Année Collège

Durée :45 min

Barème :20 points

Exercice 1 : Questions de cours (4 points)

4 pts

1) Énoncer le théorème de Pythagore direct. (1 pt)

2) Énoncer la réciproque du théorème de Pythagore. (1 pt)

3) Dans un triangle rectangle, comment appelle-t-on le côté opposé à l’angle droit ? (1 pt)

4) Dans un triangle ABC rectangle en A, écrire la relation de Pythagore. (1 pt)

Exercice 2 : Application directe (4 points)

4 pts

Soit $EFG$ un triangle rectangle en $E$ tel que $EF = 5$ cm et $EG = 3$ cm.

1) Faire une figure. (1 pt)

2) Calculer $FG$. (2 pts)

3) Donner la valeur exacte puis une valeur approchée au dixième près. (1 pt)

Exercice 3 : Réciproque du théorème de Pythagore (4 points)

4 pts

On considère un triangle $ABC$ tel que :

$AB = 2\sqrt{2}$ cm, $AC = \sqrt{3}$ cm et $BC = \sqrt{5}$ cm.

1) Quel est le plus grand côté de ce triangle ? (1 pt)

2) Calculer les carrés des trois côtés. (1 pt)

3) Montrer que $ABC$ est un triangle rectangle en précisant le sommet de l’angle droit. (2 pts)

Exercice 4 : Relations métriques (4 points)

4 pts

Soit $ABC$ un triangle rectangle en $A$. $H$ est le pied de la hauteur issue de $A$ sur l’hypoténuse $[BC]$.

On donne : $BH = 4$ cm et $CH = 9$ cm.

1) Calculer $AH$. (1 pt)

2) Calculer $AB$. (1 pt)

3) Calculer $AC$. (1 pt)

4) Calculer l’aire du triangle $ABC$. (1 pt)

Exercice 5 : Synthèse (4 points)

4 pts

Soit $ABC$ un triangle isocèle rectangle en $A$, avec $AB = 4$ cm. Soit $M$ le milieu du segment $[BC]$.

1) Faire une figure. (1 pt)

2) Calculer $BC$. (1 pt)

3) Calculer $AM$. (2 pts)

🔒 Abonnez-vous pour accéder à la correction de cette évaluation.

Je m’abonne maintenant

Modèle N°1

Exercice 1：(10pts)

Le quadrilatère BOIS est un carré de côté 12 cm .

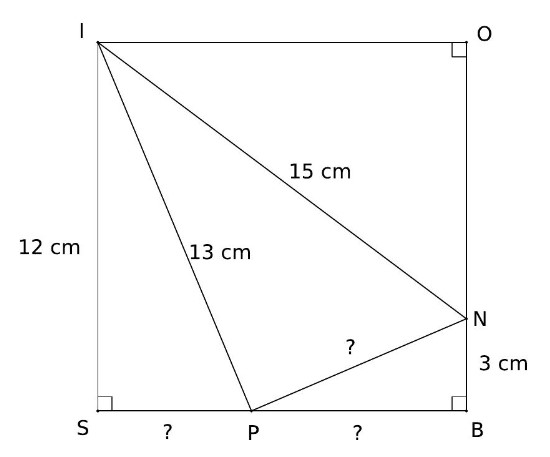
1) Calculer la longueur $S P$.

2) Calculer la longueur $P N$ et en donner une valeur arrondie au mm.

3) Le triangle PIN est-il rectangle?

Exercice 2：(5pts)

Une balle en plastique de 74 mm de diamètre, a laissé une trace dans le sable, de 24 mm de diamètre.

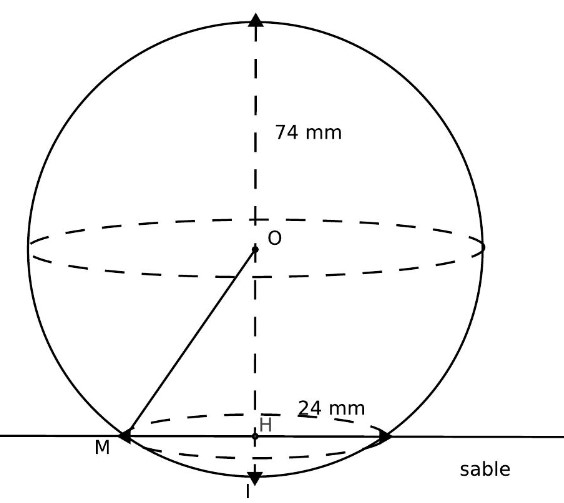
1) Calculer les longueurs $O M, O I$ et $H M$.

2) Calculer la longueur $O H$, et en déduire à quelle profondeur la balle s’est enfoncée.

Exercice 3：(5pts)

1) Construire un triangle $A B C$ tel que $A B=8 \mathrm{~cm}, \widehat{B A C}=63^{\circ}$ et $\widehat{A B C}=27^{\circ}$.

2) Placer le point $D$ sur $[B C]$ avec $B D=4 \mathrm{~cm}$, puis construire le triangle $B D E$ tel que $D E=2 \mathrm{~cm}$ et $B E=4,5 \mathrm{~cm}$.
(placer $E$ du même côté que $A$ et $B$ par rapport à $(B C)$ )

3) Les droites $(A C)$ et $(E D)$ sont-elles parallèles? (justifier)

Théorème de Pythagore – Évaluations corrigés