Les exercices corrigés sur Le théorème de Thalès en classe
Exercice 1:
Ajuster la propriété de Thalès à chaque configuration de Thalès :
$1)$
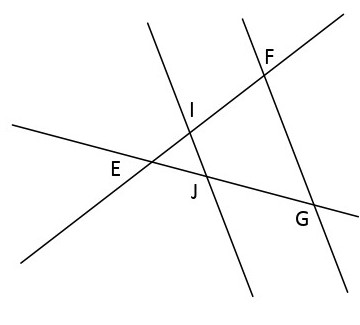
$2)$
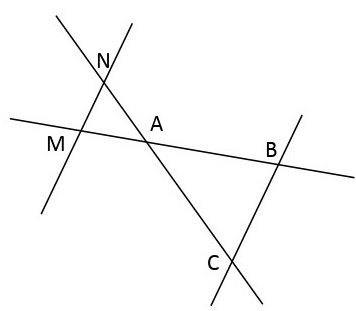
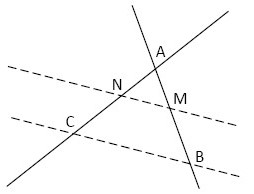
$1)$ $(FI)$ et $(GJ)$ sont sécantes en $E$.
Puisque $(FG) // (IJ)$ alors d’après le théorème de Thalès:
$\frac{\mathbf{E I}}{\mathbf{E F}}=\frac{\mathbf{E J}}{\mathbf{E G}}=\frac{\mathbf{I J}}{\mathbf{F G}}$
$2)$ $(NC)$ et $(BM)$ sont sécantes en $A$.
Puisque $(MN) // (BC)$ alors d’après le théorème de Thalès :
$\frac{\mathbf{A M}}{\mathbf{A B}}=\frac{\mathbf{A N}}{\mathbf{A C}}=\frac{\mathbf{M N}}{\mathbf{B C}}$
Exercice 2:
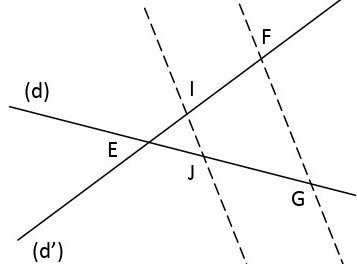
Les droites en pointillés sont toujours parallèles. Écrire dans chaque cas l’égalité des rapports, puis calculer la longueur manquante (éventuellement arrondie au dixième) :
$1)$ $\mathrm{EI}=2,4$; $\mathrm{EF}=6$; $\mathrm{EJ}=3$
Calculer $EG$ :
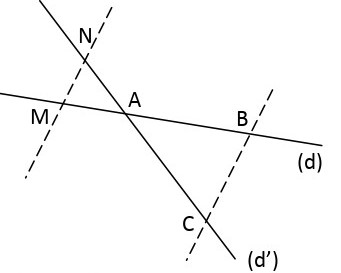
$2)$ $A M=4,3 ; A B=7,9 ; A C=8,8$
Calculer $AN$ :
$1)$ $\mathrm{EI}=2,4$; $\mathrm{EF}=6$; $\mathrm{EJ}=3$
$(IF)$ et $(GJ)$ sont sécantes en $E$
Puisque $(IJ) // (FG)$ alors d’après le théorème de Thalès :
$\frac{\mathbf{E I}}{\mathbf{E F}}=\frac{\mathbf{E J}}{\mathbf{E G}}=\frac{\mathbf{I J}}{\mathbf{F G}} $
$\frac{\mathbf{2 , 4}}{\mathbf{6}}=\frac{\mathbf{3}}{\mathbf{E G}}$
$\mathbf{E G}=\frac{6 \times 3}{2,4}=7,5$
$2)$ $(C N)$ et (BM) sont sécantes en $A$ .
Puisque $(BC) // (MN)$ alors d’après le théorème de Thalès :
$\frac{\mathrm{AN}}{\mathrm{AC}}=\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{NM}}{\mathrm{CB}} $
$\frac{\mathrm{AN}}{8,8}=\frac{4,3}{7,9}$
$\mathbf{A N}=\frac{4,3 \times 8,8}{7,9} \approx 4,8$
Exercice 3:
Démontrer (si c’est le cas) que les deux droites en pointillés sont parallèles, en tenant compte des indications chiffrées (données en cm) de chaque figure et en utilisant la réciproque de Thalès :
$1)$ $A M=7 ; A B=8 ; A N=8,4 ; A C=9,6$
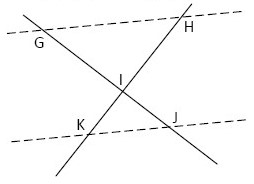
$2)$ $\mathrm{IJ}=5$; $\mathrm{IG}=8$; $\mathrm{IK}=6$; $\mathrm{KH}=15,6$
$1)$ $A M=7 ; A B=8 ; A N=8,4 ; A C=9,6$
D’une part : $\quad \frac{A M}{A B}=\frac{7}{8}=0,875$
D’autre part: $\quad \frac{\mathrm{AN}}{\mathrm{AC}}=\frac{8,4}{9,6}=0,875$
Puisque $\frac{A M}{A B}=\frac{A N}{A C}$ et puisque les points $A, M, B$ et $A, N, C$ sont alignés dans le même ordre, alors d’après la réciproque de Thalès: $(MN)//(BC)$
$2)$ $ \frac{\mathbf{I K}}{\mathbf{I H}}=\frac{6}{15,6-6}=0,625$
D’autre part : $ \frac{\mathbf{I J}}{\mathbf{I G}}=\frac{5}{8}=0,625 $
Puisque : $\frac{\mathbf{I K}}{\mathbf{I H}}=\frac{\mathbf{I J}}{\mathbf{I G}}$ et puisque les points $I, K, H$ et $I, J, G$ sont alignés dans le même ordre, alors d’après la réciproque de Thalès : $(GH) // (JK)$
Exercice 4:
Sur le dessin ci-dessous, les droites (AB) et (CD) sont parallèles ; les droites (AC) et (BD) sont sécantes en $O$.
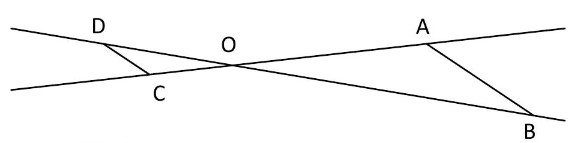
On donne :
$\mathrm{OA}=8 \mathrm{~cm}$
$\mathrm{OB}=10 \mathrm{~cm}$
$O C=2 \mathrm{~cm}$
$\mathrm{DC}=1,5 \mathrm{~cm}$
$1)$ Calculer la longueur du segment $[A B]$.
$2)$ Calculer la longueur du segment [OD].
$1)$ Les droites $(A C)$ et ( $B D)$ se coupent en $O$ et $(A B) / /(C D)$ D’après le théorème de Thalès :
$\frac{O A}{O C}=\frac{O B}{O D}=\frac{A B}{C D}$
$\frac{8}{2}=\frac{10}{O D}=\frac{A B}{1,5}=4$
$\mathbf{A B}=\frac{8 \times 1,5}{2}=4 \times 1,5=6 \mathrm{~cm}$
$2)$ $\quad \mathbf{O D}=\frac{2 \times 10}{8}=2,5 \mathrm{~cm}$
Exercice 5: Le théorème de Thalès
Sur la figure ci-après, tracée à main levée :
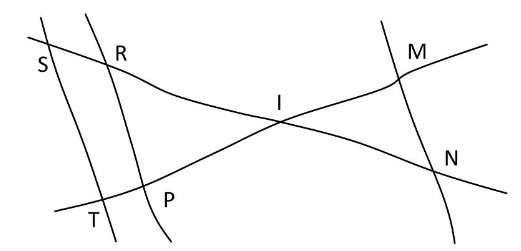
$I R=8 \mathrm{~cm} \quad R P=10 \mathrm{~cm} \quad I P=4 \mathrm{~cm}$
$I M=4 \mathrm{~cm} \quad I S=10 \mathrm{~cm} \quad I N=6 \mathrm{~cm} \quad I T=5 \mathrm{~cm}$
On ne demande pas de refaire la figure.
$1)$ Démontrer que les droites $(ST)$ et $(RP)$ sont parallèles.
$2)$ En déduire $S T$.
$3)$ Les droites $(MN)$ et $(ST)$ sont-elles parallèles ? Justifier.
$1)$ $\frac{\mathbf{I R}}{\mathbf{I S}}=\frac{8}{10}=0,8$ et $\frac{\mathbf{I P}}{\mathbf{I T}}=\frac{4}{5}=0,8$
Ainsi : $\frac{\mathbf{I R}}{\mathbf{I S}}=\frac{\mathbf{I P}}{\mathbf{I T}}$
et les points $I, R, S$ et $I, P, T$ sont alignés dans le même ordre.
D’après la réciproque de Thalès : $(ST) // (RP)$
$2)$ Les droites $(RS)$ et $(PT)$ se coupent en I et $(PR) // (ST)$
D’après le théorème de Thalès :
$\frac{\text { IR }}{\text { IS }}=\frac{\text { IP }}{\text { IT }}=\frac{\text { RP }}{\text { ST }} \Leftrightarrow \frac{8}{10}=\frac{10}{\text { ST }}$
$\mathbf{S T}=\frac{10 \times 10}{8}=12,5 \mathrm{~cm}$
$3)$ $\frac{\text { IM }}{\mathrm{IT}}=\frac{4}{5}=0,8$ et $\frac{\mathbf{I N}}{\mathrm{IS}}=\frac{6}{10}=0,6$
Ainsi $: \frac{\text { IM }}{\text { IT }} \neq \frac{\text { IN }}{\text { IS }}$ :
la réciproque de Thalès ne s’applique pas: les droites $(MN)$ et $(ST)$ ne sont pas parallèles.
Exercice 6:
L’unité est le centimètre.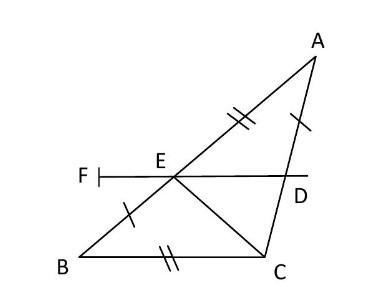
On considère le triangle $A B C$.
Soit $E$ un point du segment $[A B]$; la parallèle à la droite $(BC)$ passant par E coupe le segment $[A C]$ au point $D$.
On donne $A E=B C=3$ et $E B=A D=2$.
$1)$ Montrer que $E D=1,8$.
$2)$ Sur la demi-droite $[DE)$, on place, comme indiqué sur la figure ci-contre, le point $F$ tel que $D F=3$.
Les droites $(A D)$ et $(B F)$ sont-elles parallèles ?
$1)$ Les droites $(BE)$ et $(CD)$ se coupent en $A$ et $(BC) // (DE)$
D’après le théorème de Thalès :
$\frac{\mathrm{AE}}{\mathrm{AB}}=\frac{\mathrm{AD}}{\mathrm{AC}} =\frac{\mathrm{ED}}{\mathrm{BC}}$
$ \Leftrightarrow \frac{3}{3+2}=\frac{2}{2+\mathrm{DC}}=\frac{\mathrm{ED}}{3} $
$\frac{3}{5} =\frac{\mathrm{ED}}{3} \Leftrightarrow \mathbf{E D}=\frac{3 \times 3}{5}=1,8 \mathrm{~cm}$
$2)$ $\frac{\mathbf{E D}}{\mathbf{E F}}=\frac{1,8}{3-1,8}=\frac{1,8}{1,2}=1,5$ et $\frac{\mathbf{E A}}{\mathbf{E B}}=\frac{3}{2}=1,5$
Ainsi : $\frac{E D}{E F}=\frac{E A}{E B}$ et les points $E, D, F$ et $E, A, B$ sont alignés dans le même ordre.
D’après la réciproque de Thalès : $(AD) // (BF)$
Exercice 7:
Calculer la valeur exacte de $ST$ en utilisant les informations données.
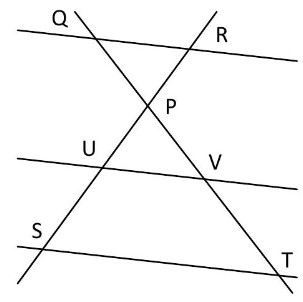
$\mathrm{RP}=4 \mathrm{~cm} $
$ \mathrm{QR}=2,4 \mathrm{~cm} $
$ \mathrm{PV}=2 \mathrm{~cm} $
$ \mathrm{PS}=4,5 \mathrm{~cm} $
$ (\mathrm{QR}) / /(\mathrm{UV}) $
$ (\mathrm{UV}) / /(\mathrm{ST})$
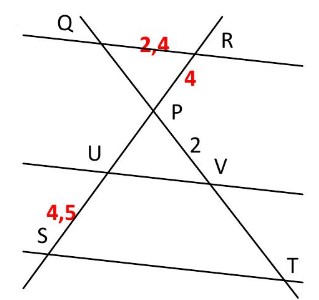
Les droites $(RS)$ et $(QT)$ se coupent en $P$ et $(QR) // (ST)$
D’après le théorème de Thalès :
$\frac{\mathbf{P S}}{\mathbf{P R}} =\frac{\mathbf{P T}}{\mathbf{P Q}}=\frac{\mathbf{S T}}{\mathbf{R Q}} \Leftrightarrow \frac{\mathbf{4 , 5}}{\mathbf{4}}=\frac{\mathbf{S T}}{\mathbf{2 , 4}} $
$ \Leftrightarrow \mathbf{S T}=\frac{4,5 \times 2,4}{4}=2,7 \mathrm{~cm}$
Exercice 8:
La figure ci-dessous représente un champ rectangulaire $A B C D$ traversé par une route de largeur uniforme (partie grise).
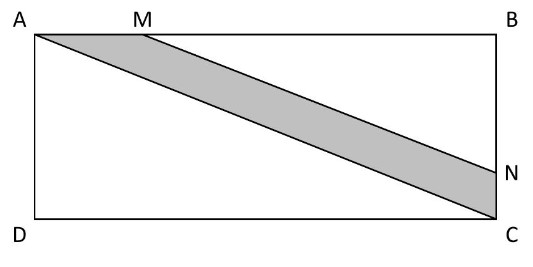 – On donne : $\mathrm{AB}=100 \mathrm{~m} \quad \quad \mathrm{BC}=40 \mathrm{~m} \quad \quad \mathrm{AM}=24 \mathrm{~m}$
– On donne : $\mathrm{AB}=100 \mathrm{~m} \quad \quad \mathrm{BC}=40 \mathrm{~m} \quad \quad \mathrm{AM}=24 \mathrm{~m}$
– Les droites $(AC)$ et$ (MN)$ sont parallèles.
Calculer :
$1)$ La valeur arrondie au décimètre prés de la longueur $AC$.
$2)$ La longueur $MB$.
$3)$ La longueur $ BN$.
$1)$ Calcul de $AC$ :
Le triangle $A B C$ est rectangle en $B$.
D’après le théorème de Pythagore :
$A C^{2}=A B^{2}+B C^{2}=100^{2}+40^{2}=11600 $
$ A C=\sqrt{11600} \simeq 107,7 \mathrm{~m}$
$2)$ Calcul de $\mathrm{MB}: \mathbf{M B}=\mathrm{AB}-\mathrm{AM}=\mathbf{1 0 0}-\mathbf{2 4}=\mathbf{7 6} \mathrm{m}$
$3)$ Calcul de $BN$ :
Les droites $(AM)$ et $(CN)$ se coupent en $B$ et $ (AC) // (MN) $ D’après le théorème de Thalès :
$\frac{B M}{B A}=\frac{B N}{B C}=\frac{M N}{A C} \Leftrightarrow \frac{76}{100}=\frac{B N}{40}=\frac{M N}{107,7} $
$ \Leftrightarrow B N=\frac{76 \times 40}{100}=30,4 \mathrm{~m}$
Exercice 9:
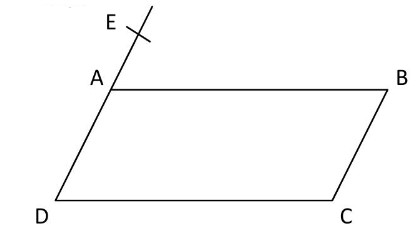
$A B C D$ est un parallélogramme :
– $A B=8 \mathrm{~cm} \quad A D=4,5 \mathrm{~cm}$;
– $\quad$ est le point de la droite $(AD)$ tel que $A E=1,5 \mathrm{~cm}$ et $E$ n’est pas sur le segment $[AD]$;
– la droite $(EC)$ coupe le segment $[AB]$ en $M$.
$1)$ Calculer $AM$.
$2)$ Placer le point $N$ sur le segment $[D C]$ tel que :
$\mathrm{DN}=\frac{3}{4} \mathrm{DC}$
• Démontrer que les droites $(AN)$ et $(EC)$ sont parallèles.
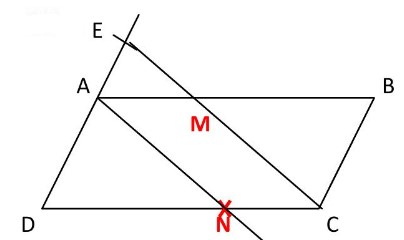
$1)$ Calculer $AM$.
Les droites $(AD)$ et $(MC)$ se coupent en $E$ et $(AM) // (BC)$ D’après le théorème de Thalès :
$\frac{E A}{E D}=\frac{E M}{E C}=\frac{A M}{D C} \Leftrightarrow \frac{1,5}{1,5+4,5}=\frac{E M}{E C}=\frac{A M}{8} $
$\frac{1,5}{6}=\frac{A M}{8} \Leftrightarrow A M=\frac{8 \times 1,5}{6}=2 \mathrm{~cm}$
$2)$ Placer le point $N$ sur le segment $[DC]$ tel que :
$D N=\frac{3}{4} D C$
$\frac{\mathrm{DA}}{\mathrm{DE}}=\frac{4,5}{6}=0,75$
et $\frac{\mathrm{DN}}{\mathrm{DC}}=\frac{3}{4}=0,75$
Ainsi : $\frac{D A}{D E}=\frac{D N}{D C}$ et les points $D, A, E$ et $D, N, C$ sont alignés dans le même ordre.
D’après la réciproque de Thalès : $(AN) // (EC)$.
Exercice 10:
$1)$ Tracer un segment $[E F]$ tel que $E F=10 \mathrm{~cm}$ puis un demi-cercle de diamètre $[EF]$.
Sur ce demi-cercle, placer le point $G$ tel que $E G=9 \mathrm{~cm}$.
Sur le segment $[EG]$, placer le point $M$ tel que $\mathrm{EM}=8 \mathrm{~cm}$.
Par $M$ tracer la droite $(d)$ perpendiculaire à la droite $(EG)$, les droites $(d)$ et $(EF)$ se coupent en $P$.
$2)$ Démontrer que les droites $(FG)$ et $(MP)$ sont parallèles.
$3)$ Calculer $EP$.
$1)$
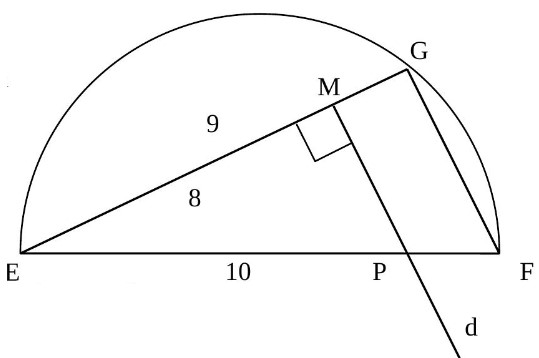
$2)$ Le point $G$ appartient au cercle de diamètre [EF].
Or si on joint un point d’un cercle aux extrémités d’un diamètre alors on forme un angle droit en se point.
donc $(\mathrm{EG}) \perp(\mathrm{GF})$
De plus: (EG) $\perp$ (GF) et (EG) $\perp$ (MP)
Or si deux droites sont perpendiculaires à une même droite alors elles sont parallèles entre elles. donc $(GF) // (MP)$
$3)$ Dans les triangles $EMP$ et $EGF $ on a : $G∈(EM) , F∈(EP) , (GF) // (MP)$
Donc d’après le théorème de Thalès on a :
$\frac{E M}{E G}=\frac{E P}{E F}$
Soit : $\frac{8}{9}=\frac{E P}{10}$
D’où : $8×10=EP×9$
Ainsi : $E P=\frac{80}{9} \approx 8,89 \mathrm{~cm}$.
Exercice 11:
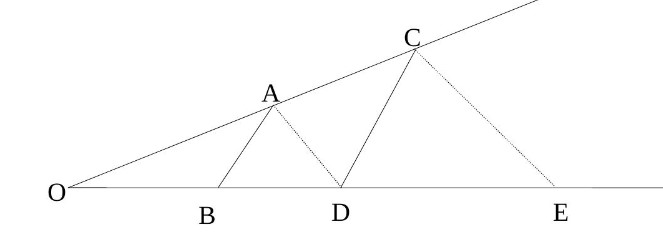
On donne : $\mathrm{OA}=4 \mathrm{~cm}$ ; $\mathrm{OB}=5 \mathrm{~cm}$
$\mathrm{BD}=3 \mathrm{~cm}$
$(\mathrm{AB}) / /(\mathrm{CD})$
$(\mathrm{AD}) / /(\mathrm{CE})$
• Calculer $AC$ et $DE$.
• Les droites $(BD)$ et $(AC)$ se coupent en $O$ et $(AB)$ $/ /(\mathrm{CD})$
D’après le théorème de Thalès : $\frac{O B}{O D}=\frac{O A}{O C}$
Soit : $\frac{5}{5+3}=\frac{4}{O C}$, d’où : $5 \times O C=8 \times 4$
Ainsi : $O C=\frac{32}{5}=6,4 \mathrm{~cm}$.
Les points $\mathrm{O}, \mathrm{A}, \mathrm{C}$ sont alignés donc :
$\mathrm{AC}=\mathrm{OC}-\mathrm{OA}=6,4-4=2,4$
La longueur $A C$ est de $2,4 \mathrm{~cm}$.
.
• Les droites $(AC)$ et $(DE)$ se coupent en $O$ et $(AD) // (CE)$
D’après le théorème de Thalès : $\frac{O D}{O E}=\frac{O A}{O C}$
Soit : $\frac{8}{O E}=\frac{4}{6,4}$, d’où : $4 \times O E=8 \times 6,4$
Ainsi : $O E=\frac{51,2}{4}=12,8 \mathrm{~cm}$.
Les points $O, D, E$ sont alignés donc :
$\mathrm{DE}=\mathrm{OE}-\mathrm{OD}=12,8-8=4,8$
La longueur $DE$ est de $4,8 \mathrm{~cm}$.
Exercice 12:
Des bateaux participent à une régate. Ils doivent suivre le parcours suivant (en gras et fléché sur la figure ci-dessous) :
On donne:
$\quad-\mathrm{FM}=10 \mathrm{~km}$
$\quad – DF = 6 km$
$\quad- MA = 2 × DM $
$\quad- \widehat{FDM}=90^{\circ}$
$\quad- F ∈ (DG) \quad et \quad M ∈ (DA)$
– les droites $(FM)$ et $(AG)$ sont parallèles.
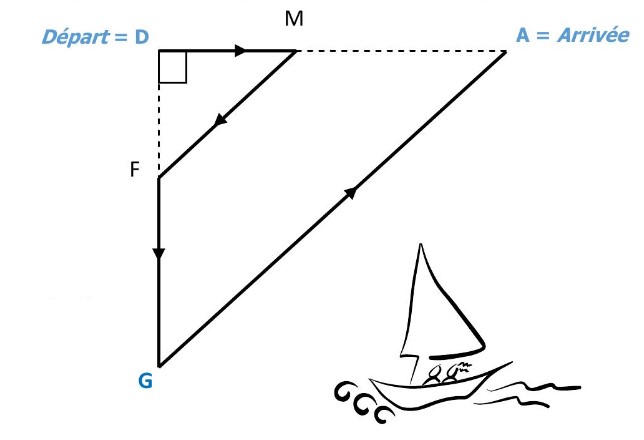
$1)$ Calcule $DM$.
$2)$ Calcule $AG$ et $FG$.
$3)$ Déduis-en la longueur de la régate.
$1)$ Le triangle DMF est rectangle en D. Or, d’après le théorème de Pythagore, on a :
$\mathrm{FM}^{2} =\mathrm{DF}^{2}+\mathrm{DM}^{2} $
$10^{2} =6^{2}+\mathrm{DM}^{2} $
$\mathrm{DM}^{2} =100-36 $
$\mathrm{DM}^{2} =64 $
$\mathrm{DM} =\sqrt{64} $
$\mathrm{DM} =8 \mathrm{~km}$
$2)$ D’une part les points $F, D, G$ et d’autre part les points $M$, $D$, A sont alignés.
Les droites $(FM)$ et $(AG)$ sont parallèles.
Or, d’après le théorème de Thalès :
$\frac{D M}{D A}=\frac{D F}{D G}=\frac{F M}{A G}$
$\frac{8}{24}=\frac{6}{\mathrm{DG}}=\frac{10}{\mathrm{AG}} \quad \mathrm{DA}=\mathrm{DM}+\mathrm{MA}=\mathrm{DM}+2 \times \mathrm{DM}=3 \times \mathrm{DM}=3 \times 8=24 \mathrm{~km}$.
$\mathrm{DG}=\frac{24 \times 6}{8}=18 \mathrm{~km} \quad$
Donc $\quad \mathrm{FG}=\mathrm{DG}-\mathrm{DF}=18-6=12 \mathrm{~km}$
$\frac{8}{24}=\frac{6}{\mathrm{DG}}=\frac{10}{\mathrm{AG}} \quad$
D’où $\quad \mathrm{AG}=\frac{24 \times 10}{8}=30 \mathrm{~km}$.
$3)$ $\mathrm{DM}+\mathrm{FM}+\mathrm{FG}+\mathrm{AG}=8+10+12+30=60$
La longueur de la régate est $60 km$ .
Les exercices corrigés sur Le théorème de Thalès en classe
