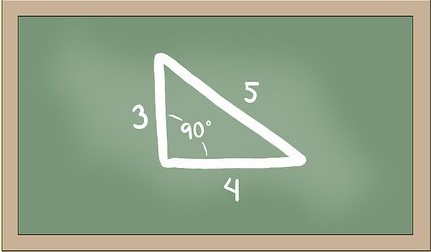
Introduction au triangle 3 4 5
Le triangle 3 4 5 est un triangle particulier qui possède des propriétés intéressantes et qui est utilisé dans de nombreuses applications géométriques.
Dans cet article, nous allons explorer en détail ce triangle et tout ce qu’il faut savoir pour le maîtriser. Que vous soyez étudiant en mathématiques ou simplement curieux de découvrir les secrets du triangle , vous êtes au bon endroit.
Comprendre les propriétés du triangle 3 4 5
Le triangle est un triangle rectangle, ce qui signifie qu’il possède un angle droit. En plus de cela, il a des côtés dont les longueurs sont dans une relation spécifique : le côté opposé à l’angle droit mesure 3 unités, le côté adjacent à l’angle droit mesure 4 unités, et l’hypoténuse mesure 5 unités. Cette relation est ce qui rend le triangle unique et intéressant.
Les propriétés du triangle peuvent être utilisées pour résoudre différents problèmes géométriques. Par exemple, connaissant les longueurs des côtés, nous pouvons facilement calculer l’aire du triangle en utilisant la formule de l’aire d’un triangle : aire = (base * hauteur) / 2.
Dans le cas du triangle , la base et la hauteur sont respectivement les côtés de longueur 3 et 4, ce qui nous donne une aire de (3 * 4) / 2 = 6.
Applications du triangle 3 4 5 en géométrie
Le triangle trouve de nombreuses applications dans la géométrie. Par exemple, il peut être utilisé pour déterminer si un triangle avec des longueurs de côtés données est un triangle rectangle. Si les longueurs des côtés sont en proportion 3:4:5, alors le triangle est un triangle rectangle.
De plus, le triangle peut être utilisé pour construire d’autres triangles avec des rapports de côtés similaires. En utilisant les propriétés du triangle , nous pouvons construire un triangle avec des côtés de longueurs 6, 8 et 10, ou un triangle avec des côtés de longueurs 9, 12 et 15, et ainsi de suite.
Cette technique de construction de triangles est très utile dans de nombreux problèmes géométriques.
Comment construire un triangle 3 4 5
La construction d’un triangle est assez simple. Vous aurez besoin d’une règle graduée et d’un compas pour effectuer cette construction. Voici les étapes à suivre :
- Tracez une ligne droite avec votre règle graduée, qui servira de base pour le triangle.
- Placez la pointe sèche de votre compas sur un point de la ligne droite, et ouvrez le compas jusqu’à ce qu’il mesure 3 unités.
- Tracez un arc de cercle à partir du point où vous avez placé la pointe sèche du compas.
- Déplacez la pointe sèche du compas sur l’arc de cercle que vous avez tracé, et ouvrez le compas jusqu’à ce qu’il mesure 4 unités.
- Tracez un autre arc de cercle à partir du point où vous avez placé la pointe sèche du compas.
- Les deux arcs de cercle se croiseront en deux points. Reliez ces points avec votre règle graduée pour obtenir le côté de longueur 5 du triangle.
- Vous avez maintenant construit un triangle 3 4 5.
Théorème de Pythagore et le triangle 3 4 5
Le théorème de Pythagore est une relation mathématique fondamentale qui s’applique aux triangles rectangles. Il énonce que dans un triangle rectangle, le carré de l’hypoténuse (le côté opposé à l’angle droit) est égal à la somme des carrés des deux autres côtés.
Dans le cas du triangle 3 4 5, nous pouvons vérifier le théorème de Pythagore. L’hypoténuse du triangle mesure 5 unités, et les carrés des côtés de longueurs 3 et 4 sont respectivement 9 et 16.
Si nous additionnons ces deux carrés, nous obtenons 9 + 16 = 25, ce qui est égal au carré de l’hypoténuse. Ainsi, le triangle satisfait bien le théorème de Pythagore.
Exemples concrets du triangle 3 4 5
Pour mieux comprendre l’utilisation du triangle , examinons quelques exemples concrets.
Exemple 1: Supposons que vous ayez un terrain rectangulaire avec une largeur de 3 mètres et une hauteur de 4 mètres. Vous voulez construire une clôture pour entourer le terrain.
En utilisant le triangle , vous pouvez calculer la longueur de la clôture en utilisant le théorème de Pythagore. L’hypoténuse du triangle sera la longueur de la clôture, qui est égale à √(3^2 + 4^2) = 5 mètres.
Exemple 2: Vous avez une échelle de 5 mètres de long et vous voulez l’appuyer contre un mur de manière à ce qu’elle forme un angle de 90 degrés avec le sol.
En utilisant le triangle , vous pouvez trouver la distance entre le mur et le pied de l’échelle. La distance sera de 3 mètres, car c’est la longueur du côté adjacent à l’angle droit.
Conseils pour résoudre les problèmes impliquant le triangle 3 4 5
Lorsque vous êtes confronté à des problèmes impliquant le triangle , voici quelques conseils utiles pour vous aider à les résoudre :
- Vérifiez d’abord si les longueurs des côtés sont en proportion 3:4:5. Si c’est le cas, vous savez que vous avez affaire à un triangle rectangle.
- Utilisez le théorème de Pythagore pour vérifier si le triangle satisfait cette relation fondamentale.
- Si vous avez besoin de calculer l’aire du triangle, utilisez la formule de l’aire d’un triangle en utilisant les côtés de longueurs 3 et 4 comme base et hauteur.
- Si vous devez construire d’autres triangles avec des rapports de côtés similaires, utilisez les propriétés du triangle pour effectuer la construction.
Autres types de triangles et leurs relations avec le triangle 3 4 5
Il existe de nombreux autres types de triangles qui ont des relations avec le triangle. Par exemple, le triangle 6 8 10 est un multiple du triangle 3 4 5, où toutes les longueurs de côtés sont doublées. De même, le triangle 9 12 15 est un autre multiple du triangle.
De plus, le triangle peut être utilisé pour construire des triangles équilatéraux. En utilisant les propriétés du triangle , nous pouvons construire un triangle équilatéral en utilisant le côté de longueur 5 du triangle comme base.
Faits amusants et anecdotes sur le triangle 3 4 5
Le triangle a une longue histoire et a été étudié par de nombreux mathématiciens au fil des siècles. Il est intéressant de noter que le triangle a été utilisé dans l’architecture égyptienne ancienne pour construire des pyramides.
Les constructeurs égyptiens utilisaient la relation de longueur des côtés du triangle pour s’assurer que les côtés de la pyramide étaient parfaitement droits.
Un autre fait amusant est que le triangle est également connu sous le nom de « triangle de Pythagore », en référence au célèbre mathématicien grec Pythagore.
Pythagore a étudié les propriétés des triangles rectangles, et le triangle est l’un des triangles rectangles les plus simples et les plus connus.
Conclusion : Maîtriser l’art du triangle 3 4 5
En conclusion, le triangle est un triangle particulier avec des propriétés intéressantes et de nombreuses applications géométriques. En comprenant les propriétés du triangle , en utilisant le théorème de Pythagore et en connaissant les techniques de construction, vous pouvez maîtriser l’art du triangle.
Que vous soyez étudiant en mathématiques ou simplement curieux de découvrir les secrets de ce triangle, le triangle offre une fascinante exploration de la géométrie. Alors plongez-vous dans l’étude du triangle et découvrez les merveilles qu’il a à offrir.