Introduction :
Les triangles sont des figures géométriques fascinantes qui ont captivé l’attention des mathématiciens, des artistes et des penseurs depuis des siècles.
Parmi ces triangles, le triangle 6 8 10 se distingue par une harmonie géométrique parfaite et des propriétés remarquables.
Dans cet article, nous explorerons les caractéristiques uniques de ce triangle et son importance dans le monde des mathématiques et au-delà.
Les côtés du Triangle 6 8 10 :
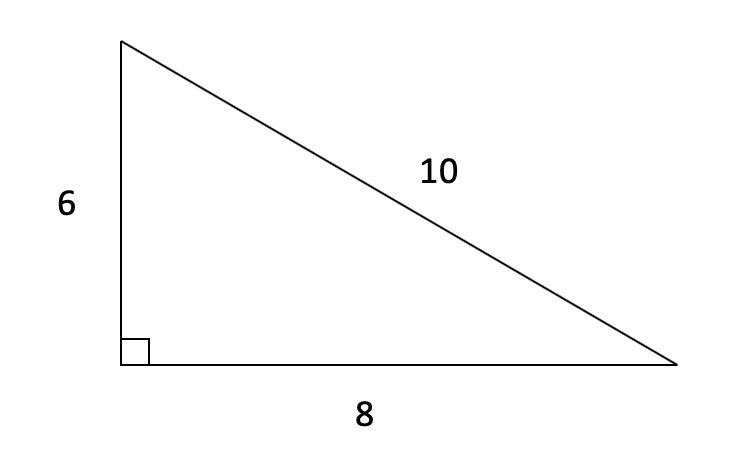
Le triangle est défini par ses côtés de longueurs spécifiques : un côté de longueur 6 unités, un autre de 8 unités et le troisième de 10 unités.
Ces longueurs forment une proportion simple et harmonieuse qui donne à ce triangle des propriétés intéressantes.
Propriétés du Triangle 6-8-10 :
Relation Pythagoricienne :
Le triangle est un triangle rectangle, ce qui signifie qu’il obéit à la célèbre relation pythagoricienne. En effet, la somme des carrés des deux côtés les plus courts (6² + 8²) est égale au carré du côté le plus long (10²).
6² + 8² = 10²
Cette propriété est fondamentale et illustre la liaison profonde entre la géométrie et l’algèbre.
Multiples de Pythagore :
Le triangle est également intéressant car il est un multiple entier d’un autre triangle pythagoricien célèbre, le triangle 3 4 5.
En multipliant tous les côtés du triangle 3 4 5 par 2, on obtient le triangle.
2 × ( 3 − 4 − 5 ) = 6 − 8 − 10
Cela montre comment le triangle est lié à des concepts plus larges dans la théorie des nombres.
Utilisations Pratiques :
Le triangle a des applications pratiques, notamment dans la construction et la menuiserie. Lors de la création d’un triangle rectangle avec des côtés de longueurs 6, 8 et 10 unités, il est possible de s’assurer que les angles du triangle sont droits, ce qui est essentiel dans de nombreux projets de construction.
Conclusion :
Le triangle , avec ses propriétés pythagoriciennes et son harmonie géométrique, est une figure mathématique intrigante. Son lien avec d’autres triangles pythagoriciens et ses applications pratiques en font un sujet d’étude intéressant pour les passionnés de mathématiques .
Ce triangle, simple en apparence, offre une richesse de concepts qui continuent d’inspirer la fascination pour la géométrie et les mathématiques.
