Les triangles sont des formes géométriques fascinantes qui revêtent une importance cruciale dans divers domaines mathématiques et scientifiques. Parmi les différentes catégories de triangles, le triangle acutangle offre une richesse de propriétés intrigantes et trouve des applications significatives dans divers contextes.
Dans cet article, nous plongerons dans les caractéristiques du triangle acutangle, tout en explorant ses implications et son utilité.
Définition et Propriétés
1. Définition :

Un triangle acutangle est défini par l’ensemble de ses trois angles intérieurs, qui sont tous aigus, c’est-à-dire inférieurs à 90 degrés. La somme totale des angles de ce triangle est toujours égale à 180 degrés.
2. Propriétés Distinctives :
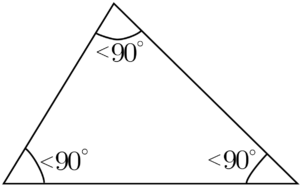
Angles Aigus : Chacun des trois angles intérieurs est inférieur à 90 degrés, conférant au triangle une apparence pointue et élancée.
Longueurs des Côtés : Les côtés du triangle acutangle peuvent varier en longueur, mais l’élément clé réside dans la nature aiguë de ses angles.
Les Applications Pratiques du Triangle Acutangle
1. Trigonométrie :
Les triangles acutangles jouent un rôle central dans la trigonométrie (le cas d’un angle de 90°). Les rapports trigonométriques tels que le sinus, le cosinus et la tangente sont définis en fonction des côtés d’un triangle, et ces relations sont souvent explorées dans le contexte des triangles acutangles.
2. Géométrie Analytique :
En géométrie analytique, les propriétés des triangles acutangles peuvent être utilisées pour résoudre des systèmes d’équations linéaires et explorer les relations entre les points dans le plan cartésien.
3. Modélisation Mathématique :
Les triangles acutangles sont couramment utilisés pour modéliser divers phénomènes dans les sciences et l’ingénierie, tels que la résolution de problèmes liés à la géodésie, à la navigation et aux calculs d’angles dans des applications technologiques.
Conclusion :
Une Exploration Enrichissante Le triangle acutangle, avec ses angles pointus et ses applications diversifiées, offre une perspective fascinante sur le monde de la géométrie.
Comprendre ses propriétés et ses utilisations pratiques peut non seulement enrichir nos connaissances mathématiques, mais également éclairer son importance dans des domaines tels que la trigonométrie et la modélisation mathématique.
En somme, le triangle acutangle se révèle être bien plus qu’une simple figure géométrique ; il incarne la puissance des mathématiques dans notre compréhension du monde qui nous entoure.
