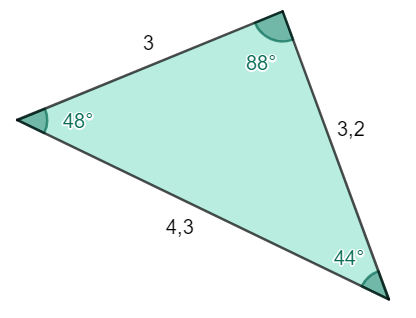
Introduction :
Les triangles, formes géométriques de base, revêtent une diversité étonnante. Parmi cette variété, le triangle scalène acutangle se distingue par sa singularité et son élégance.
Dans cet article, nous explorerons les caractéristiques spécifiques de ce triangle, sa nature acutangle et les implications de sa géométrie unique.
Définition du Triangle Scalène Acutangle :
Un triangle est dit scalène lorsque ses trois côtés ont des longueurs différentes. Ajoutez à cela le qualificatif « acutangle », et vous obtenez un triangle dont tous les angles internes sont aigus, c’est-à-dire mesurant moins de 90 degrés.
Caractéristiques du Triangle Scalène Acutangle :
Variété des Longueurs des Côtés :
Contrairement aux triangles équilatéraux ou isocèles, où au moins deux côtés ont des longueurs égales, le triangle scalène acutangle se distingue par la disparité de ses côtés. Cette diversité contribue à sa flexibilité géométrique.
Angles Aigus :
Chacun des trois angles internes du triangle mesure moins de 90 degrés. Cette caractéristique en fait un triangle particulièrement adapté à la modélisation de situations où des angles aigus sont nécessaires.
Flexibilité dans la Construction :
En raison de ses côtés de longueurs différentes, le triangle offre une flexibilité accrue dans la construction géométrique.
Cette propriété en fait un choix intéressant pour diverses applications, de l’architecture à la conception artistique.
Applications du Triangle Scalène Acutangle :
Géométrie Appliquée :
Les triangles scalènes acutangles sont fréquemment utilisés dans la géométrie appliquée pour modéliser des situations réelles où des angles aigus sont impliqués, comme dans l’arpentage, la cartographie et la conception d’objets.
Art et Design :
Les artistes et les designers peuvent exploiter la flexibilité géométrique du triangle pour créer des compositions visuellement intéressantes.
Sa nature asymétrique offre des possibilités infinies pour jouer avec l’équilibre et la variété.
Conclusion :
Le triangle par sa nature diversifiée et ses angles aigus, offre une perspective fascinante dans le monde de la géométrie.
Sa présence dans des domaines aussi variés que la science, l’art et l’ingénierie témoigne de sa polyvalence et de son importance.
En embrassant la beauté de la variété, ce triangle nous rappelle que la géométrie, loin d’être statique, est une source infinie d’inspiration et de créativité.