Introduction :
Dans le vaste royaume de la géométrie, l’angle droit émerge comme une entité fondamentale, une boussole visuelle guidant notre compréhension de l’espace.
En définissant des relations angulaires spécifiques, l’angle droit joue un rôle central dans divers domaines, de l’architecture à la navigation en passant par les concepts mathématiques.
Cet article explore la signification profonde de cet angle , mettant en lumière son influence omniprésente.
Définition de l’Angle Droit :
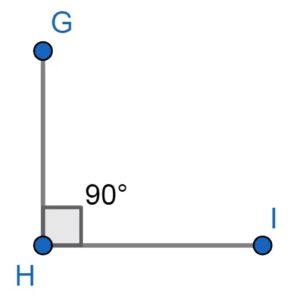
Un angle droit est défini comme un angle dont la mesure est précisément de 90 degrés, soit un quart du tour complet d’un cercle.
L’angle est souvent représenté par un petit carré ou une petite boîte à l’intersection de deux lignes, symbolisant ainsi sa caractéristique distinctive.
Caractéristiques de l’Angle Droit :
Mesure Fixe :
L’angle droit se distingue par sa mesure fixe de 90 degrés, ce qui le rend prévisible et facile à identifier visuellement.
Formation dans les Intersections :
Les angles droits se forment naturellement lorsque deux lignes droites se croisent. Ces intersections, présentes dans des configurations variées, sont essentielles pour définir des repères dans l’espace.
Utilité dans la Géométrie :
L’angle est un élément clé de nombreuses constructions géométriques. Il est utilisé dans la définition de formes et de figures, facilitant la résolution de problèmes mathématiques et la création de structures précises.
Rôle de l’Angle Droit dans la Géométrie :
Théorème de Pythagore :
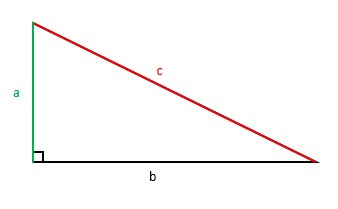
L’angle est au cœur du célèbre théorème de Pythagore. Dans un triangle rectangle, deux des côtés forment cet angle , et la somme des carrés de ces côtés est égale au carré de l’hypoténuse.
a² + b² = c²
Construction Précise :
Les angles droits sont largement utilisés dans la construction et l’architecture pour garantir la précision des formes et des structures. Les bâtiments, les ponts et d’autres ouvrages reposent souvent sur des fondations géométriques définies par ces angles .
Navigation et Cartographie :
En navigation et en cartographie, où la précision des directions est cruciale, l’utilisation d’angles droits facilite la création de cartes précises et la détermination de positions relatives.
Conclusion :
L’angle droit, avec sa mesure fixe de 90 degrés, est bien plus qu’une simple abstraction géométrique. C’est un outil fondamental qui guide notre compréhension de l’espace et de la forme.
Que ce soit dans les fondements mathématiques, la construction de structures imposantes ou la cartographie du monde qui nous entoure, l’angle demeure une clé de compréhension essentielle.
Apprécier son rôle omniprésent nous permet d’explorer et de comprendre le tissu même de notre environnement géométrique.