Droites dans le plan parallélisme et perpendicularité

I. Point, droite, demi-droite et segment :

1. Droite :

Propriété 1 : 

Par deux points distinctes $M$ et $N$ passe une et une seule droite notée $(MN)$ ou $(NM)$.

Exemple : 

Propriété 2 : 

Par un point il passe une infinité de droites.

Exemple : 

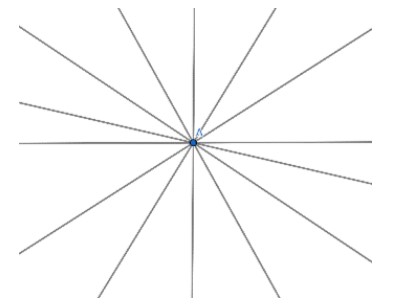
2. Demi-droites opposées : 

Définition  :

Deux demi-droites opposées sont deux demi-droites différentes qui ont :

• Même origine

• Même support

• Un seul point commun qui est l’origine

Exemple : 

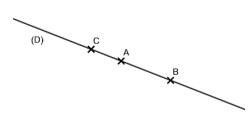
Les demi-droites $[AB)$ et $[AC)$ sont opposés :

• Même origine $A$

• Même support $(D)=(AB)=(AC)$

• Un seul point commun

II. Appartenance, alignement :

1.  Appartenance :

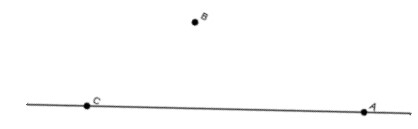
2. Points alignés :

Définition  : 

Les points alignés sont des points qui appartiennent à une même droite.

Exemple : 

Les points $A, B$ et $C$ sont alignés Mais $A, B$ et $D$ ne sont pas alignés

3. Milieu d’un segment :  

Définition 1 :

Deux segments qui ont même longueur sont égaux Autrement dit ils sont isométriques.

Exemple : 

Les segments $[AB]$ et $[CD]$ sont égaux (isométriques)

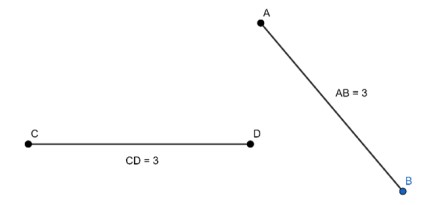
Définition 2 :

Le milieu d’un segment est le point de ce segment qui est équidistant à ses extrémités.
Autrement dit : $M$ milieu de $[AB]$ signifie que $M ∈ [AB]$ et $MA = MB$  .

Exemple : 

Le point $M$ est le milieu de $[AB]$  :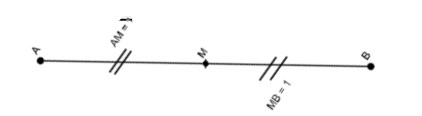

III. Positions de deux droites :

1. Droites sécantes :

Définition  :

Deux droites sécantes sont deux droites qui n’ont qu’un seul point commun.

Exemple : 

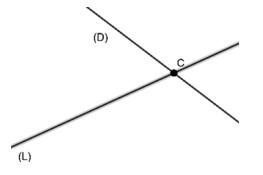
Les deux droites $(D)$ et $(L)$ sont sécantes (se coupent en $C$)

2. Droites perpendiculaires :

Définition  :

Deux droites perpendiculaires sont deux droites sécantes qui forment quatre angles droits.

Propriété : 

Par un point donné passe une et une seule droite perpendiculaire à une droite donnée.

Projection orthogonale : Le point $H$ pied de la perpendiculaire est appelé la projection orthogonale du point $C$ sur la droite $(L)$.

La longueur du segment  $[CH ]$ est appelée la distance entre le point $C$ et la droite $(L)$ et c’est la plus petit de $C$ à n’importe quel point de $(L)$

Exemple : 

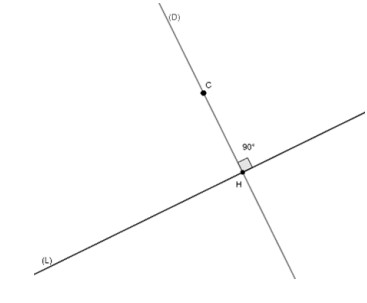
Les deux droites $(D)$ et $(L)$ sont perpendiculaire, et notées $(D) \perp (L)$
ou $(L) \perp (D)$

$H$ est la projection orthogonale du point $C$ sur la droite $(L)$

3. Droites parallèles :

Définition  :

Deux droites parallèles sont deux droites non sécantes.

Deux droites confondues sont aussi parallèles .

Propriété : 

Par un point donné passe une et une seule droite parallèle à une droite donnée.

Exemple : 

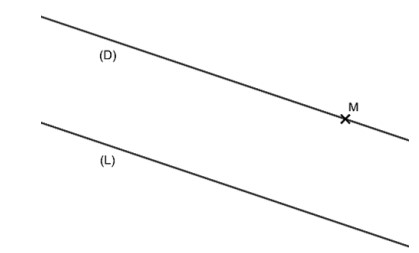
Les deux droites $(D)$ et $(L)$ sont parallèles, et notées $(D) // (L)$ ou  $(L) // (D)$

IV. Propriétés de trois droites :

Propriété 1 : 

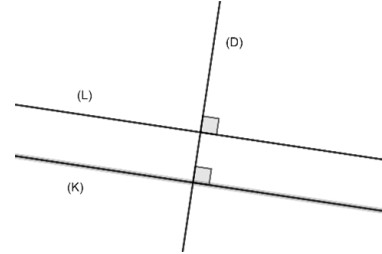
Lorsque deux droites sont parallèles, toute perpendiculaire à l’une est perpendiculaire à l’autre.

Exemple : 

On a $(K) // (L)$ et $(D) \perp (L)$  alors $(D) \perp (K)$

Propriété 2 : 

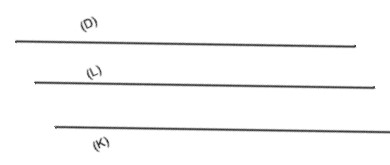
Lorsque deux droites sont parallèles, toute droite parallèle à l’une est parallèle à l’autre.

Exemple : 

On a $(K) // (L)$ et $(D) // (L)$  alors  $(K) // (D)$

Propriété 3 : 

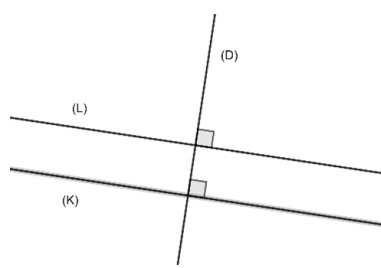
Lorsque deux droites sont perpendiculaires, toute droite perpendiculaire à l’une est parallèle à l’autre.

Exemple : 

On a $(K) \perp (D)$ et $(L) \perp (D)$  alors  $(K) // (L)$

Propriété 4 : 

Lorsque deux droites sont perpendiculaires, toute droite parallèle à l’une est perpendiculaire à l’autre.

Exemple : 

On a $(K) // (L)$ et $(D) \perp (K)$  alors  $(D) \perp (L)$