Droites dans le plan parallélisme et perpendicularité – Évaluations

Évaluation de Mathématiques

Droites dans le plan – Parallélisme et Perpendicularité

Matière :Mathématiques

Niveau :1^ère Année Collège

Durée :45 min

Barème :20 points

Exercice 1 : Vocabulaire et notations (4 points)

4 pts

1) Compléter les phrases suivantes :

a) Par deux points distincts, il passe une … droite. (0,5 pt)

b) Par un point, il passe une … de droites. (0,5 pt)

c) Des points sont dits … s’ils appartiennent à la même droite. (0,5 pt)

d) Le … d’un segment est le point équidistant des extrémités. (0,5 pt)

2) Traduire en langage mathématique les phrases suivantes :

a) Le point M appartient à la droite (AB). (0,5 pt)

b) Les droites (D) et (L) sont perpendiculaires. (0,5 pt)

c) Les droites (K) et (H) sont parallèles. (0,5 pt)

d) Les points A, B et C sont alignés. (0,5 pt)

Exercice 2 : Appartenance et alignement (4 points)

4 pts

On considère la figure ci-dessous où les points sont placés sur une même droite (D).

1) Dire si les affirmations suivantes sont vraies ou fausses :

a) $B \in (AE)$ (0,5 pt)

b) $C \notin (BE)$ (0,5 pt)

c) $A$, $C$ et $E$ sont alignés (0,5 pt)

d) $D$ est le milieu de $[BE]$ (0,5 pt)

2) Si $B$ est le milieu de $[AC]$, $AB = 3$ cm, calculer $AC$. (1 pt)

3) Si $C$ est le milieu de $[BD]$, $CD = 4$ cm, calculer $BC$ et $BD$. (1 pt)

Exercice 3 : Positions de deux droites (4 points)

4 pts

On considère les droites $(D_1)$, $(D_2)$, $(D_3)$ et $(D_4)$ telles que :

$(D_1) \perp (D_2)$, $(D_3) // (D_1)$ et $(D_4) \perp (D_3)$.

1) Quelle est la position relative de $(D_1)$ et $(D_3)$ ? (1 pt)

2) Quelle est la position relative de $(D_2)$ et $(D_4)$ ? Justifier. (1,5 pts)

3) Que peut-on dire de $(D_2)$ et $(D_3)$ ? Justifier. (1,5 pts)

Exercice 4 : Construction et propriétés (4 points)

4 pts

1) Construire une droite $(D)$ et placer un point $A$ n’appartenant pas à $(D)$.

a) Tracer la droite $(d_1)$ passant par $A$ et perpendiculaire à $(D)$. (1 pt)

b) Tracer la droite $(d_2)$ passant par $A$ et parallèle à $(D)$. (1 pt)

2) Que peut-on dire des droites $(d_1)$ et $(d_2)$ ? Justifier. (1 pt)

3) Soit $(d_3)$ une droite passant par $A$ et perpendiculaire à $(d_1)$. Que peut-on dire de $(d_3)$ et $(D)$ ? Justifier. (1 pt)

Exercice 5 : Synthèse (4 points)

4 pts

On considère la figure ci-dessous où :

$(D_1) \perp (D_2)$, $(D_3) // (D_1)$ et $(D_4) \perp (D_3)$.

1) Démontrer que $(D_2) // (D_4)$. (2 pts)

2) Démontrer que $(D_2) \perp (D_3)$. (2 pts)

Modèle $N°1$

Exercice 1 : (Questions de cours) Compléter : $(3 pts)$

Si deux droites ne sont pas parallèles alors on dit qu’elles sont $……………………………………$

Si deux droites sont parallèles alors une perpendiculaire à l’une est $…………………………………….$

Si deux droites sont parallèles alors une parallèle à l’une est $…………………………………………….$

Deux droites perpendiculaires sont aussi $…………………………………………………..$

Si deux droites sont perpendiculaires alors une parallèle à l’une est $…………………………………….$

Si deux droites sont perpendiculaires alors une perpendiculaire à l’une est $……………….…………….$

Exercice 2 : Observer chaque figure puis $(2 pts)$

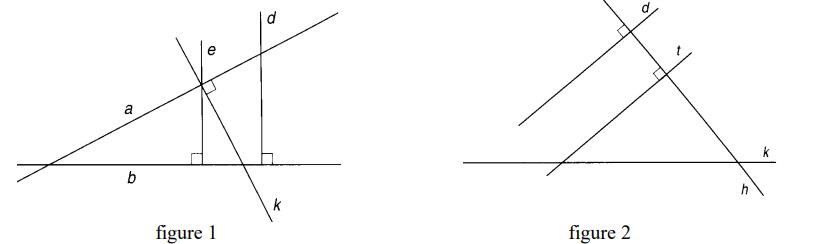
Figure $1$

Compléter les phrases avec «parallèles» ou «perpendiculaires» ou «sécantes»

Les droites $(a)$ et $(b)$ sont $\qquad$

Les droites $(a)$ et $(k)$ sont $\qquad$

Les droites $(e)$ et $(d)$ sont ……………………….

Figure $2$

Compléter les lignes suivantes avec les symboles « $\perp$ » ou «$//$ » ou «$X$» (ce dernier symbole sera utilisé pour traduire le mot «sécantes»).

$(d)$ $……$ $(t) $

$(h)$ $\ldots \ldots$ $(k)$

$(t)$ $\ldots \ldots$ $(h)$

Exercice 3 : $(2 pts)$

Dans chacun des cas suivants, tracer la droite $(d’)$ parallèle à la droite $(d)$ passant par le point $A$.

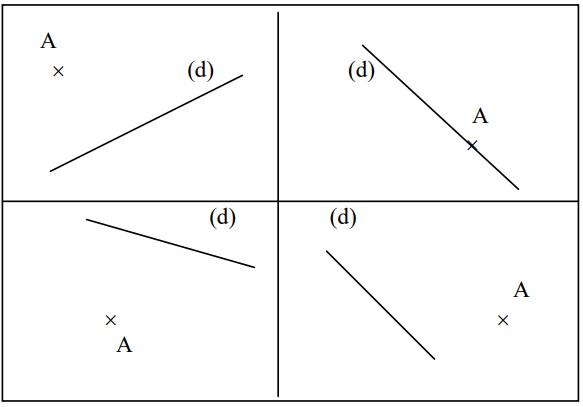
Exercice 4 : $(2 pts)$

$1)$ Placer trois points $A$,$ S$ et $M$ qui ne soient pas alignés.

$2)$ Tracer ensuite : $[AM]$ en rouge, $(SM)$ en vert et $[AS)$ en bleu.

$3)$ Tracer en noir la perpendiculaire à $(SM)$ passant par $A$

$4)$ Tracer la parallèle à $(AS)$ en $M$.

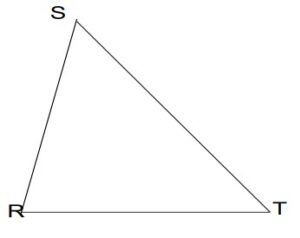
Exercice 5 : $(2 pts)$

$1)$ Tracer la perpendiculaire à $(RS)$ passant par $T$

$2)$ Tracer la parallèle à $(ST)$ passant par $R$.

Exercice 6 : (2 pts)

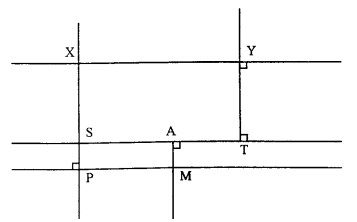
Sur la figure ci-contre, que peut-on dire des droites $(AM)$ et $(YT)$ ? Justifier en complétant le raisonnement suivant :

On sait que ………………………………………………. …………………………………………………………….

Propriété : ………………………………………………..…………………………………………………………….

Donc ………………………………………………………

Exercice 7 : $(2 pts)$

Reproduire cette figure en respectant les indications (les points $A, B$ et $C$ sont alignés) :

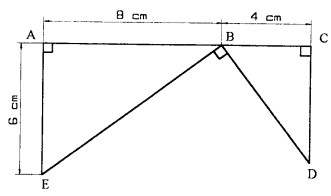
Exercice 8 : $(5 pts)$

$ABC$ est un triangle.

$M$ est le milieu du segment $[AB]$.

$1)$ Placer avec soin le point $M$.

$2)$ Tracer la parallèle à $(BC)$ passant par $M$ elle coupe $[AC]$ en $N$.

$3)$ Tracer la parallèle à $(AB)$ passant par $N$ elle coupe $[BC]$ en $P$.

$4)$ Tracer la parallèle à $(AC)$ passant par $P$ elle coupe $[AB]$ en $R$.
(Si tes tracés sont précis, vous remarquerez que les points R et M sont confondus).

$5)$ Tracer la droite $(Δ)$, perpendiculaire à $(MN)$ et passant par $A$.

Que pouvez-vous dire des droites $(Δ)$ et $(BC)$ ? Justifier votre réponse.

🔒 Abonnez-vous pour accéder à la correction détaillée de cette évaluation

Je m’abonne maintenant

Droites dans le plan parallélisme et perpendicularité – Évaluations