Théorème de Pythagore

I- Théorème de Pythagore direct

Théorème de Pythagore direct

Proposition

Dans un triangle rectangle, le carré de la longueur de son hypoténuse est égale à la somme des carrées des longueurs des côtés de l’angle droit.

Autrement dit: Si $ A B C$ est un triangle rectangle en $A$, alors : $A B^{2}+A C^{2}=B C^{2}$

• Figure géométrique :

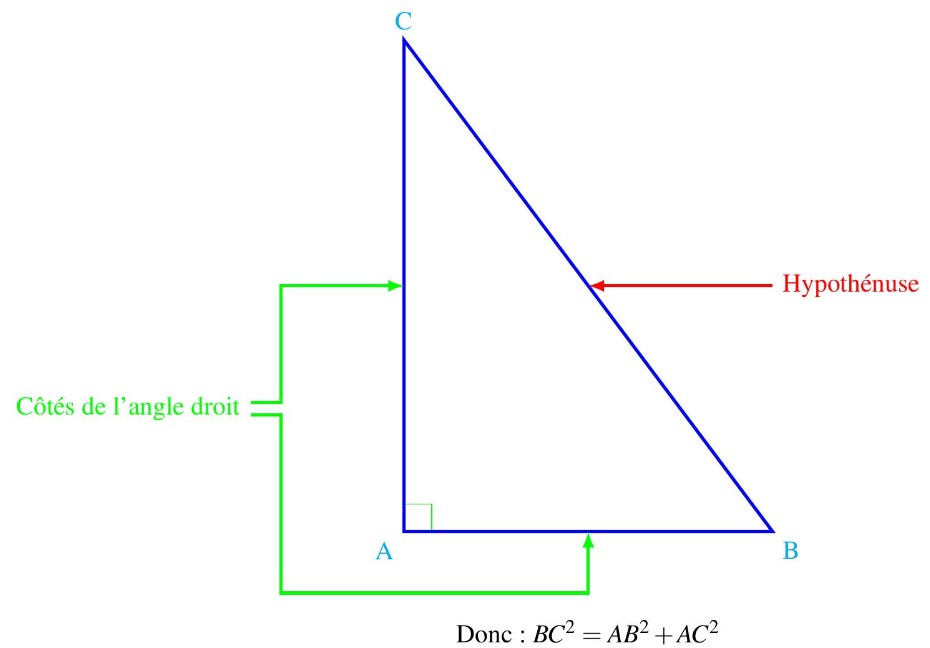
$A B C$ est un triangle rectangle en $A$

Remarque
$\star A B C$ est un triangle rectangle en $A$, donc $B C^{2}=A B^{2}+A C^{2}$

Alors : $\left\{\begin{array}{l}A B^{2}=B C^{2}-A C^{2} \\ A C^{2}=B C^{2}-A B^{2}\end{array}\right.$

$\star$ On utilise le théorème de Pythagore pour calculer les longueurs

Exemple

Soit $E F G$ un triangle rectangle en $E$ tel que : $E F=5$ et $E G=3$
Calculer $F G$

Solution

On a $E F G$ est un triangle rectangle en $E$,

Donc d’après le théorème de Pythagore direct, on a : $F G^{2}=E F^{2}+E G^{2}$

C’est à dire : $F G^{2}=5^{2}+3^{2}$

Donc: $F G^{2}=25+9$

            $F G^{2}=34$

D’ou : $F G=\sqrt{34}$

Application

Soit $A B C$ un triangle isocèle et rectangle en $A$, tel que : $A B=4 \mathrm{~cm}$ Soit $M$ le milieu de $[B C]$

1) Constuire une figure

2) Calculer $B C$

3) Déduire $A M$

Solution

1) Construisons une figure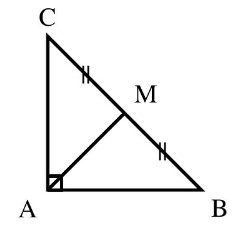

2) Calculons $B C$

On a $A B C$ est un triangle rectangle en $A$

Donc d’après le théorème de Pythagore direct, on a : $B C^{2}=A B^{2}+A C^{2}$

$C^{\prime}$ est à dire : $B C^{2}=4^{2}+4^{2}$

Donc : $B C^{2}=16+16$, donc $B C^{2}=32$

$B C=\sqrt{32}=\sqrt{16 \times 2}=\sqrt{16} \times \sqrt{2}=\sqrt{4^{2}} \times \sqrt{2}$

D’où : $B C=4 \sqrt{2}$

3) Déduisons $A M$ (En utilisant le théorème de Pythagore)

On a $A B C$ est un triangle isocèle en et $M$ le milieu de $[B C]$

Donc $(A M)$ est la médiatrice de $[B C]$

C’est à dire : $(A M) \perp(B C)$

Donc le triangle $A M B$ est rectangle en $M$

$M$ milieu de $[B C]$

Donc $B M=\frac{B C}{2}=\frac{4 \sqrt{2}}{2}=2 \sqrt{2}$

Le triangle $A M B$ est rectangle en $M$, donc d’après le théorème de Pythagore direct, on a : $A B^{2}=A M^{2}+B M^{2}$

C’est à dire $: 4^{2}=A M^{2}+(4 \sqrt{2})^{2}$

Donc $16=A M^{2}+8$

 $A M^{2}=16-8$, donc $A M^{2}=8$

 $A M=\sqrt{8}$, d’où $A M=2 \sqrt{2}$

II- Théorème réciproque de Pythagore

Théorème réciproque de Pythagore

Proposition

Dans un triangle, si le carré de la longueur du plus grand côté est égale à la somme des carrées des longueurs des côtés de l’angle droit, alors ce triangle est rectangle.

Autrement dit: Si , dans un triangle $A B C$, on a $B C^{2}=A B^{2}+A C^{2}$, alors ce triangle est rectangle en $A$

• Figure géométrique :

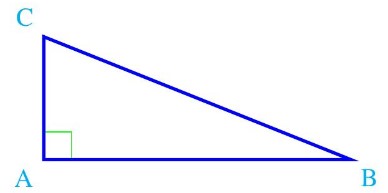
$A B C$ est un triangle tel que $B C^{2}=A B^{2}+A C^{2}$

Alors $A B C$ est un triangle rectangle en $A$

Remarque

$\star$ On utilise le théorème réciproque de Pythagore pour montrer qu’un triangle est rectangle (pour montrer la perpendicularité)

 Exemple

Soit $E F G$ un triangle tel que : $E G=6, F G=8$ et $E F=10$

Montrer que $E F G$ est un triangle rectangle en $G$

Solution

On a : $\left\{\begin{array}{l}E G^{2}=6^{2}=36 \\ F G^{2}=8^{2}=64 \\ E F^{2}=10^{2}=100\end{array}\right.$

Donc: $E G^{2}+E G^{2}=36+64=100$

Alors : $E G^{2}+E G^{2}=E F^{2}$

Donc, d’après le théorème réciproque de Pythagore, le triangle $E F G$ est rectangle en $G$

Application

Soit $A B C$ un triangle tel que : $A B=2 \sqrt{2} c m, A C=\sqrt{3}$ et $B C=\sqrt{5}$

Montrer que $A B C$ est rectangle

Solution

On a : $\left\{\begin{array}{l}A B^{2}=(2 \sqrt{2})^{2}=8 \\ A C^{2}=\sqrt{3}^{2}=3 \\ B C^{2}=\sqrt{5}^{2}=5\end{array}\right.$

On a : $A C^{2}+B C^{2}=3+5=8$

Donc : $A C^{2}+B C^{2}=A B^{2}$

Donc, d’après le théorème réciproque de Pythagore, $A B C$ est un triangle rectangle en $C$

– Paragraphe supplémentaire: Les relations métriques

${A B C}$ est un triangle rectangle en $A$ et $H$ est le projeté orthogonal du point $A$ sur $(B C)$

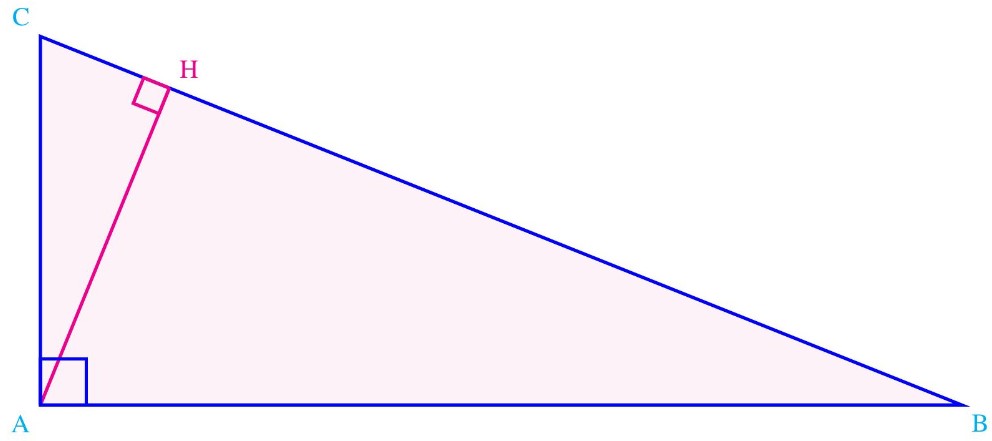
• $A B \times A C=A H \times B C$

• $A B^{2}=B H \times B C$

• $A C^{2}=C H \times B C$

• $A H^{2}=B H \times C H$