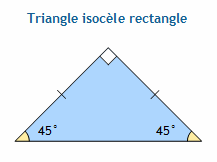
Le triangle isocèle rectangle est une figure géométrique fascinante qui possède des propriétés uniques et des applications pratiques dans divers domaines.
Dans cet article, nous explorerons les différentes caractéristiques de ce triangle, ainsi que ses utilisations dans la géométrie et dans la vie quotidienne.
Nous examinerons également les liens entre les triangles isocèles rectangles et les autres types de triangles, et nous apprendrons comment construire ce triangle.
Introduction au triangle isocèle rectangle
Le triangle isocèle rectangle est un type spécial de triangle qui possède deux côtés de même longueur et un angle droit. En d’autres termes, il a deux angles égaux et mesure 90 degrés.
Cette combinaison de propriétés en fait une figure intéressante à étudier et à utiliser dans diverses situations.
Propriétés d’un triangle isocèle rectangle
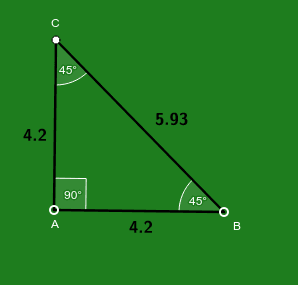
Les propriétés du triangle offrent de nombreuses possibilités de calculs et de déductions. Voici quelques-unes des caractéristiques clés de ce triangle :
- Les deux côtés de même longueur, appelés les côtés égaux, sont toujours adjacents à l’angle droit.
- L’angle formé par les côtés égaux est toujours de 45 degrés.
- La somme des angles d’un triangle isocèle rectangle est toujours de 180 degrés.
Ces propriétés permettent de déduire d’autres informations sur le triangle, telles que la longueur des côtés manquants ou les mesures des autres angles. Elles sont également utiles dans la résolution de problèmes géométriques.
Applications géométriques du triangle isocèle rectangle
Le triangle trouve des applications dans divers domaines de la géométrie. Voici quelques exemples :
Calcul de longueurs
Étant donné que les côtés égaux d’un triangle isocèle rectangle ont la même longueur, il est possible de calculer la longueur d’un côté inconnu en utilisant la longueur d’un côté connu et le théorème de Pythagore.
Cette méthode est souvent utilisée pour résoudre des problèmes de mesure de distances dans des situations réelles.
Construction de figures
Le triangle est utilisé comme élément de base pour construire d’autres figures géométriques.Par exemple, en utilisant ce triangle comme guide, il est possible de construire un pentagone régulier ou un hexagone régulier.
Trigonométrie
Les propriétés du triangle sont également utilisées dans le domaine de la trigonométrie. Les ratios trigonométriques tels que le sinus, le cosinus et la tangente peuvent être définis en utilisant les longueurs des côtés d’un triangle isocèle rectangle.
Ces concepts sont essentiels pour résoudre des problèmes de trigonométrie et sont utilisés dans de nombreux domaines tels que la navigation, l’ingénierie et l’astronomie.
Résolution de problèmes impliquant des triangles isocèles rectangles
La résolution de problèmes impliquant des triangles isocèles rectangles peut être simplifiée en utilisant les propriétés de ce triangle. Voici quelques étapes générales à suivre pour résoudre ce type de problème :
- Identifiez les informations données dans le problème, telles que les mesures des côtés ou des angles connus.
- Utilisez les propriétés du triangle isocèle rectangle pour déduire des informations supplémentaires, telles que les mesures des côtés manquants ou des angles inconnus.
- Utilisez des formules ou des théorèmes géométriques appropriés pour résoudre le problème.
- Vérifiez vos résultats en utilisant des calculs supplémentaires ou en comparant avec d’autres informations fournies dans le problème.
Applications réelles du triangle isocèle rectangle
Outre ses utilisations dans la géométrie, le triangle trouve également des applications pratiques dans la vie quotidienne. Voici quelques exemples :
Construction
Dans le domaine de la construction, ce triangle est utilisé pour s’assurer que les angles des murs et des structures sont droits.
Il est également utilisé pour mesurer les diagonales des carrés et des rectangles, ce qui peut être utile lors de la construction de meubles ou d’autres objets.
Architecture
L’architecture utilise souvent les propriétés du triangle isocèle rectangle pour créer des designs équilibrés et esthétiques. Par exemple, les façades de certains bâtiments sont conçues en utilisant des triangles isocèles rectangles pour obtenir une symétrie visuellement agréable.
Art et design
Le triangle est également utilisé dans l’art et le design pour créer des compositions visuellement intéressantes. Sa forme équilibrée et harmonieuse en fait un choix populaire pour les motifs et les arrangements géométriques.
La relation entre les triangles isocèles rectangles et les autres types de triangles
Les triangles isocèles rectangles peuvent être liés aux autres types de triangles de différentes manières. Voici quelques relations importantes :
Triangle équilatéral
Un triangle isocèle rectangle peut être considéré comme un demi-triangle équilatéral, car un de ses angles droits partage la même mesure que les angles égaux d’un triangle équilatéral.
Triangle scalène
Un triangle isocèle rectangle peut également être considéré comme un cas particulier d’un triangle scalène, qui est un triangle avec des côtés de longueurs différentes.
Dans le cas du triangle isocèle rectangle, deux des côtés sont égaux, tandis que le troisième côté est différent.
Triangle rectangle
Le triangle isocèle rectangle est un sous-ensemble du triangle rectangle. Tous les triangles isocèles rectangles sont également des triangles rectangles, mais tous les triangles rectangles ne sont pas isocèles.
Comment construire un triangle isocèle rectangle
La construction du triangle peut être réalisée en utilisant quelques étapes simples. Voici une méthode de construction :
- Tracez un segment de droite pour représenter le côté de base du triangle.
- À l’une des extrémités du segment de base, tracez un angle de 45 degrés en utilisant un rapporteur.
- À partir de l’autre extrémité du segment de base, tracez deux segments de longueur égale pour représenter les côtés égaux du triangle.
- Connectez les extrémités des côtés égaux au sommet de l’angle de 45 degrés pour former le triangle.
Conclusion
Le triangle est une figure géométrique intéressante qui possède des propriétés uniques et des applications pratiques.
En comprenant ses propriétés et ses utilisations, nous pouvons résoudre des problèmes géométriques, construire des figures complexes et trouver des applications dans divers domaines de la vie quotidienne.
Que ce soit dans la construction, l’architecture, l’art ou la trigonométrie, le triangle joue un rôle essentiel. Alors, explorez davantage ce triangle fascinant et découvrez ses multiples possibilités.
