Introduction :
Parmi la diversité infinie des triangles, le triangle scalène rectangle se distingue par son équilibre entre la variété des longueurs de côtés et la présence d’un angle droit.
Dans cet article, nous plongerons dans les caractéristiques captivantes de ce triangle, soulignant la beauté de son asymétrie et l’importance de son angle droit.
Définition du Triangle Scalène Rectangle :
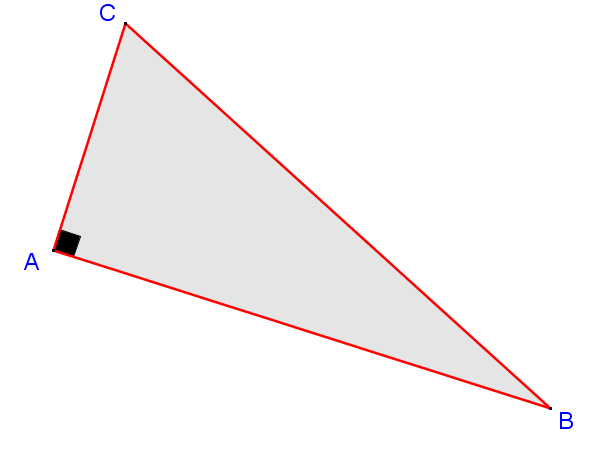
Le triangle est un triangle dont les trois côtés ont des longueurs différentes, tandis qu’un de ses angles internes mesure précisément 90 degrés, formant ainsi un angle droit.
Cette combinaison unique de propriétés géométriques offre un terrain riche en découvertes.
Caractéristiques du Triangle Scalène Rectangle :
Variété des Longueurs des Côtés :
À la différence des triangles équilatéraux ou isocèles, le triangle présente une diversité remarquable dans la longueur de ses côtés. Cette asymétrie confère au triangle une esthétique géométrique unique.
Angle Droit :
La présence d’un angle droit est l’une des caractéristiques les plus distinctives de ce triangle. Cet angle de 90 degrés a des implications profondes dans la géométrie et est fondamental dans de nombreuses applications, notamment dans le théorème de Pythagore.
Théorème de Pythagore :
Comme tout triangle rectangle, le triangle scalène rectangle obéit au célèbre théorème de Pythagore. La somme des carrés des longueurs des deux côtés les plus courts est égale au carré de la longueur du côté le plus long.
a² +b² =c²
Applications du Triangle Scalène Rectangle :
Construction et Architecture :
La présence d’un angle droit dans le triangle scalène rectangle le rend utile dans la construction et l’architecture. Les professionnels peuvent utiliser ce triangle pour garantir des angles droits précis dans leurs conceptions.
Navigation et Cartographie :
En navigation et en cartographie, où la précision des angles est cruciale, le triangle peut être utilisé pour modéliser des situations nécessitant des mesures précises.
Conclusion :
Ce triangle , en combinant la variété des longueurs de côtés avec l’ordre symétrique d’un angle droit, offre une expérience géométrique unique.
Sa présence dans des domaines aussi divers que la construction, la navigation et la cartographie témoigne de son utilité pratique.
En appréciant la symphonie harmonieuse entre asymétrie et précision, nous reconnaissons la richesse de la géométrie et l’importance du triangle dans le vaste paysage des formes géométriques.