Inégalité triangulaire et médiatrice

Inégalité triangulaire et médiatrice

I- Inégalité triangulaire :

Propriété 1

$A, B$ et $M$ étant trois points du plan,

$M \in[A B]$ signifie que : $\quad A M+M B=A B$

Exemple :

$A P+P B=A B$

Propriété 2 :

$A, B$ et $M$ étant trois points du plan,

$M \notin[A B] \quad$ signifie que : $\quad A M+M B>A B$

Exemple :

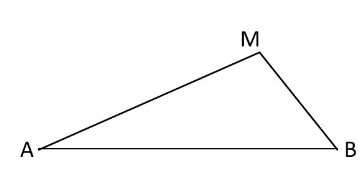
$A M+M B>A B$

Cette propriété s’appelle : inégalité triangulaire

Résultat 1 :

Dans un triangle, la longueur de chaque côté est inférieure à la la somme des longueurs des deux autres côtés.

Exemple :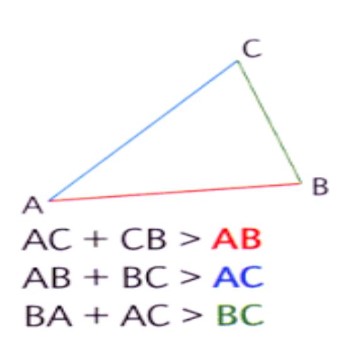

Résultat 2 :

Pour que trois nombres soient les longueurs des côtés d’un triangle, il suffit que le plus grand des trois nombres soit inférieur à la somme des deux autres nombres.

Exemple:

• $A B=3 \mathrm{~cm}, A C=4 \mathrm{~cm}$ et $B C=5 \mathrm{~cm}$

On peut construire le triangle $A B C$, car : $B C<A B+A C$

• $\mathrm{EF}=2 \mathrm{~cm}, \mathrm{EG}=3 \mathrm{~cm}$ et $\mathrm{FG}=6 \mathrm{~cm}$

On ne peut pas construire le triangle $EFG$, car : $FG > EF + EG$

II- Médiatrice d’un segment :

Définition:

La médiatrice d’un segment est une droite qui passe par le milieu de ce segment et qui est perpendiculaire à son support .

Exemple:

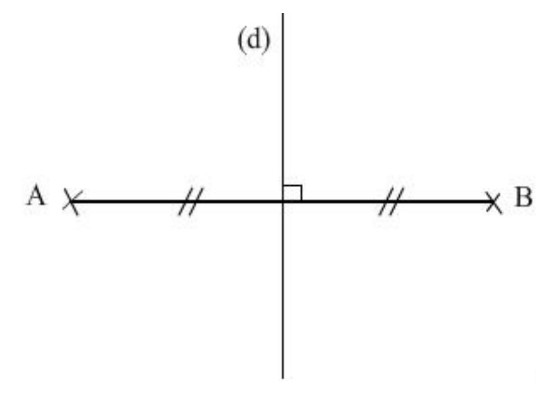
(d) est la médiatrice du segment $[A B]$

Propriété directe :

Tout point appartenant à la médiatrice d’un segment est équidistant des extrémités de ce segment.

Exemple:

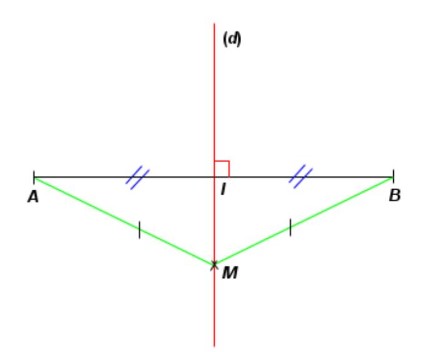
On a : (d) est la médiatrice du segment $[A B]$ et $M \in(d)$

Donc : $\quad M A=M B$

Propriété réciproque :

Tout point équidistant des extrémités d’un segment appartient à la médiatrice de ce segment.

Exemple:

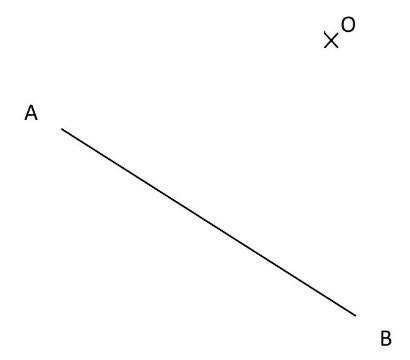
On place un point $O$ à l’extérieur du segment [AB] tel que: $O A=O B=5 \mathrm{~cm}$

Donc le point O est équidistant (à égale distance ) des extrémités du segment [AB]

Donc O appartient à la médiatrice de $[A B]$.

III- Médiatrices d’un triangle :

Définition:

La médiatrice d’un triangle est la médiatrice de l’un de ses côtés .

Définition:

Le cercle circonscrit à un triangle est le cercle qui passe par les trois sommets de ce triangle.

Propriété :

Les trois médiatrices d’un triangle se coupent en un seul point. Ce point est le centre du cercle circonscrit à ce triangle.

Exemple:

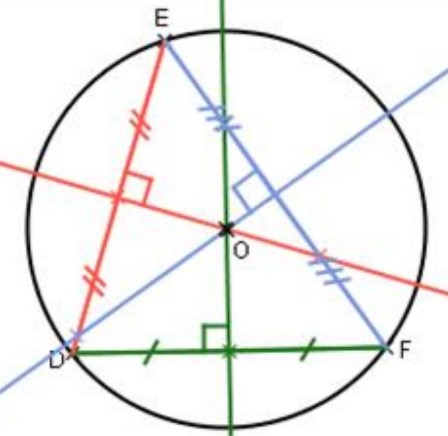
O est le centre du cercle circonscrit au triangle EFD.

Remarques :

$•$ Pour construire le cercle circonscrit à un triangle il suffit de tracer deux de ses médiatrices.

$•$ Le centre du cercle circonscrit à un triangle peut être :

– à l’intérieur du triangle lorsque tous ses angles sont aigus.
– à l’extérieur du triangle lorsque l’un de ses angles est obtus.
– sur l’un de ses côtés lorsque le triangle est rectangle.