Inégalité triangulaire et médiatrice exercices corrigés

Modèle $N°1$

Exercice 1 : $(3 pts)$

Dans chaque cas, dire si le triangle $A B C$ existe ou si les points $A, B$ et $C$ sont alignés en justifiant la réponse.

$1)$ $A B=5 \mathrm{~cm}, A C=7 \mathrm{~cm}$ et $B C=8 \mathrm{~cm}$.

$2)$ $A B=3,8 \mathrm{~cm}, A C=12,1 \mathrm{~cm}$ et $B C=8 \mathrm{~cm}$.

$3)$ $A B=3,8 \mathrm{~cm}, A C=6 \mathrm{~cm}$ et $B C=2,2 \mathrm{~cm}$.

Exercice 2 :  $(2 pts)$

Tracer le cercle circonscrit au triangle $A B C$.

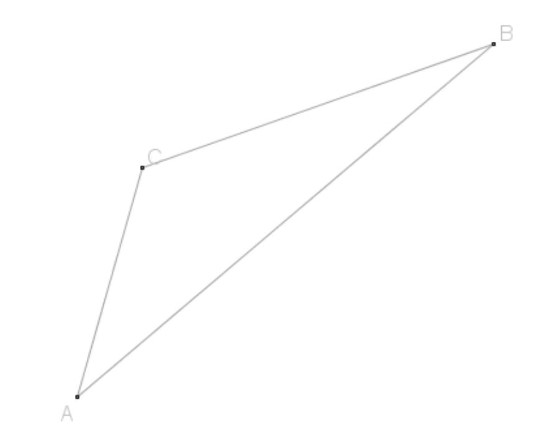
Exercice 3 :  $(2 pts)$

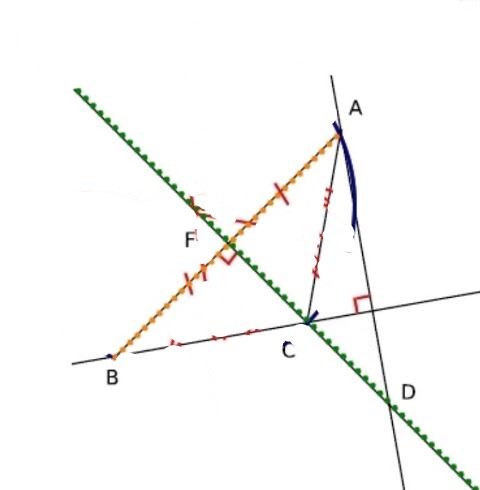
$1)$ Donner la définition de la hauteur issue de $A$ dans un triangle $A B C$.

$2)$ Que représente la droite $(F D)$ dans $A B C$ ?

$3)$ Que représente la droite $(A D)$ dans $A B C$ ?

$4)$ Construire le centre du cercle circonscrit au triangle $A B C$ et tracer ce cercle

Exercice 4 :  $(1 pts)$

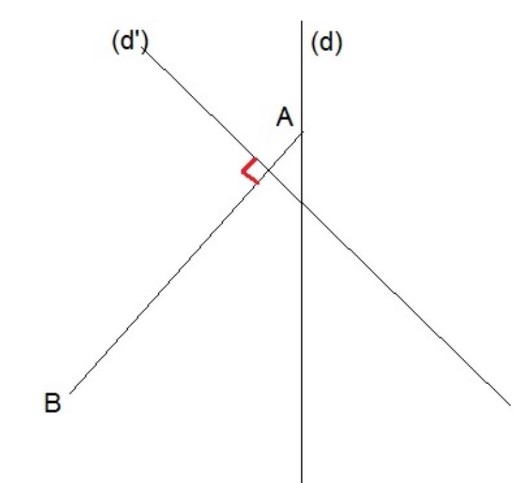
Sur la figure ci-contre la droite $(d)$ est hauteur issue de $A$ et la droite ( $d^{\prime}$ ) la hauteur issue de $C$ dans $A B C$.

• Construire le point $C$.