Nombres relatifs (Présentation et comparaison)

Nombres décimaux relatifs 

I- Introduction

Définition :

• Un nombre décimal relatif est un nombre décimal précédé d’un signe + ou –

• Les nombres positifs sont notés avec le signe + ou sans signe, ils sont plus grand que 0

• Les nombres négatifs sont notés avec le signe -, ils sont plus petit que 0

• Les nombres positifs et les nombres négatifs constituent les nombres relatifs

Exemple :

米 Les nombres $-1,13,-0.2,-27.36,5.32$ sont des nombres relatifs

光 Les nombres $-19,-103,-150.2,-207.365,-51.32$ sont des nombres relatifs négatifs

光 Les nombres $+21,+103,+0.25,+227.36,+5.302($ ou $21,103,0.25,227.36,5.302)$ sont des nombres relatifs positifs

Remarque

$\star$ Les nombres 2022, -5 sont des nombres entiers relatifs

$\star$ Les nombres $-3.2,5.4$ sont des nombres décimaux relatifs mais pas des entiers relatifs

$\star$ Le nombre 0 est à la fois positif et négatif

Application

On considère les nombres suivants : $-5;13.5;-1.5;-2;-3;0;12;+1,6 et -0.5$ 

1) Déterminer les nombres décimaux négatifs

2) Déterminer les nombres décimaux positifs

3) Déterminer les nombres entiers relatifs

Solution

1) $-1.5;-0.5$ 

2) $13.5;+1,6 $ 

3) $-5;-2;-3;0;12$ 

II- La droite graduée

1) Repérage sur une droite graduée

Définition :

On appelle droite graduée (ou axe), une droite sur laquelle on fixe :

$\cdot$ Un point $O$ appelé origine de la droite graduée

$\cdot$ Un sens

$\cdot$ Une unité de longueur

Exemple :

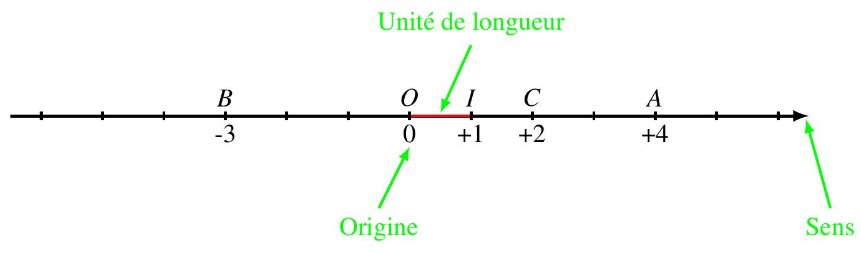
$\underset{}{*}$ L’abscisse de l’origine $O$ est le nombre 0 et l’abscisse du point $I$ est le nombre 1

Définition :

Tout point d’une droite graduée peut être repéré par un nombre relatif appelé son abscisse

Exemples :

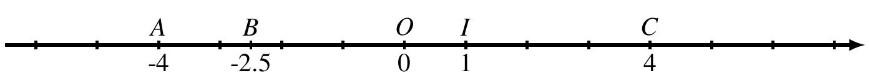
Les points $A, B$ et $C$ ont pour abscisses respectives les nombres $-4,-2.5$ et 4

On note : $A(-4), B(-2.5)$ et $C(4)$

Remarque

Les points d’abscisses négatives sont situés à gauche du point $O$, et les points d’abscisses positives sont situés à droite du point $O$

2) La distance à zéro

Définition :

La distance à zéro d’un nombre décimal relatif $a$, est la distance entre le point d’abscisse $a$, sur la droite graduée, et l’origine de la droite graduée.

Exemples :

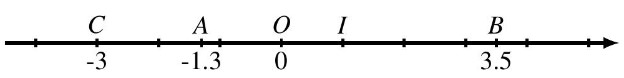
$\star$ La distance de -3 à zéro est 3 , car $O C=3$

$\star$ La distance de 3.5 à zéro est 3.5 , car $O B=3.5$

$\star$ La distance de -1.3 à zéro est 1.3 , car $O A=1.3$

3) L’opposé d’un nombre

Définition :

Deux nombres relatifs opposés sont deux nombres relatifs qui ont la même distance à zéro et des signes contraires.

Exemples :

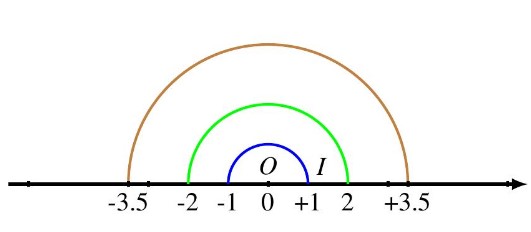
$\star$ Les nombres -3 et 3 sont opposés, car leurs distances à zéro sont égales à 3

$\star$ L’opposé de 2 est -2 et l’opposé de -1 est 1

$\star$ L’opposé du nombre décimal relatif $+a(a)$ est $-a$; donc on a : $-(+a)=-a$

$\star$ L’opposé de $-a$ est noté $-(-a)$; donc on a : $-(-a)=a$

4) Comparaison de deux nombres relatifs

a) Comparaison de deux nombres positifs

Règle :

Si deux nombres sont positifs, alors le plus grand est celui qui a la plus grande distance à zéro (C’est à dire : celui qui est le plus éloigné de zéro)

Exemple :

$+32>+13 \quad ; ; 31.63>+15.57 \quad ; ; 121<+127 \quad ; ; 1.07<107$

b) Comparaison de deux nombres négatifs

Règle :

Si deux nombres sont négatifs, alors le plus grand est celui qui a la plus petite distance à zéro (C’est à dire : celui qui est le plus prés de zéro)

c) Comparaison de deux nombres de signes différents

Règle :

Tout nombre positif est supérieur à tout nombre négatif

Exemple :

$4.27>-427 \quad ; ; \quad 6>-7 \quad ; ;-3<+5 \quad ; ; \quad-17.1<17.01$

ASTUCE

Pour ranger une série de nombres relatifs positifs et négatifs, il est conseillé de trier les nombres positifs et les nombres négatifs, puis de comparer les nombres positifs entre eux et les nombres négatifs entre eux.

Les positifs étant plus grand que les négatifs ( cas d’arangement dans l’ordre croissant )

Les négatifs étant plus petit que les positifs ( cas d’arangement dans l’ordre décroissant )

Exemple :

1) Ranger dans l’ordre croissant les nombres suivants : $-4.3 ; 4.2 ;-5 ;-4.02 ; 5 ;-7 ;-9 ; 14.5$

On relève les nombres négatifs : $-4.3 ;-5 ;-4.02 ;-7 ;-9$

On les range du plus petit au plus grand : $-9<-7<-5<-4.3<-4.02$

On relève les nombres positifs : $4.2 ; 5 ; 14.5$

On les range du plus petit au plus grand : $4.2<5<14.5$

On conclut donc : $-9<-7<-5<-4.3<-4.02<4.2<5<14.5$

2) Ranger dans l’ordre décroissant les nombres suivants : $-6.2; 6.4; -6.201; -6.221; 6.04; 6.041$

On relève les nombres positifs : $6.4 ; 6.04 ; 6.041$

On les range du plus grand au plus petit : $6.4>6.041>6.04$

On relève les nombres négatifs : $-6.2 ;-6.201 ;-6.221 \_$On les range du plus grand au plus petit : $-6.2>-6.201>-6.221$

On conclut donc : $6.4>6.041>6.04>-6.2>-6.201>-6.221$

Application

a) Comparer les nombres suivants:

(1) -2022 et -1011

(2) 53 et -11

(3) -11.3033 et -11.303

(4) -3 et 0

(5) 99.9999 et -100

b) Ranger, dans l’ordre croissant, les nombres suivants: $-3 ;-1.5 ; 3.2 ;-2 ; 0 ; 2 ; 1.6 ;-16 ;-1 ;-2.2$

Solution

a) Comparaison des nombres

(1) $-2022<-1011$

(2) $53>-11$

(3) $-11.3033<-11.303$

(4) $-3<0$

(5) $99.9999>-100$

b) Ranger, dans l’ordre croissant

$2-16<-3<-2.2<-2<-1.5<-1<0<1.6<2<3.2$