Symétrie axiale – Cours

I- Symétrique d’un point :

Définition :

Le symétrique d’un point $A$ par une symétrie axiale d’axe $(D)$ est le point $A’$ tel que $(D)$ soit la médiatrice du segment $[A A’]$.

Exemple :

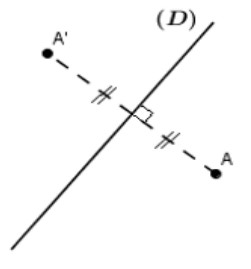
Le symétrique du point A par rapport à la droite $(D)$ est le point $A’$.

Remarque :

Si un point M appartient à la droite $(D)$ alors ce point $M$ est le symétrique de lui- ême par rapport à la droite $(D)$.

II- Symétrique d’un segment :

Propriété 1 :

Le symétrique d’un segment $[AB]$ par une symétrie axiale est un segment $[A’B’]$ de même longueur.

Exemple :

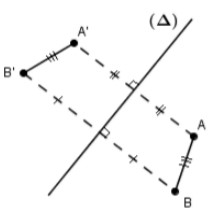
$A’$ et $B’$ sont les symétriques respectifs des points $A$ et $B$ par rapport à la droite $(∆)$.

Donc : le symétrique du segment $[AB]$ est le segment $[A’B’]$.

Propriété 2 :

La symétrie axiale conserve la distance entre deux points.

Exemple :

Dans l’exemple précédent, on a : $AB = A’B’$.

On dit que la symétrie axiale conserve la distance entre deux points.

III- Symétrique d’une droite – symétrique d’une demi-droite :

Propriété 3 :

Le symétrique d’une droite $(D)$ par une symétrie axiale est une droite $(D’)$ qui est parallèle à $(D)$.

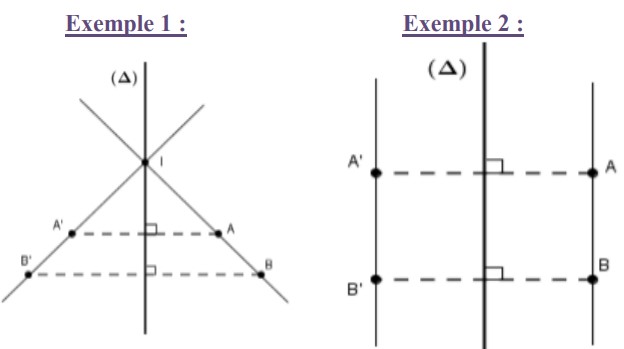
Le symétrique de la droite $(AB)$ par rapport à la droite $(∆)$ est la droite $(A’B’)$ tel que $A’$ et $B’$ sont les symétriques respectifs de $A$ et $B$ par rapport à la droite $(∆)$.

Propriété 4 :

Le symétrique d’une demi-droite $[AB)$ par une symétrie axiale est une demi-droite $[A’B’)$ tel que la droite $(AB)$ est parallèle à $(A’B’)$.

Exemple :

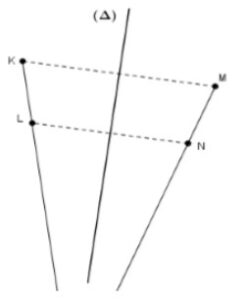
Le symétrique de la demi-droite $[MN)$ par rapport à la droite $(∆)$ Est la demi-droite $[KL)$.

Propriété 5 :

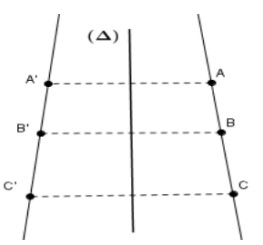
Les symétriques, par une symétrie axiale d’axe $(∆)$, de trois points alignés $A, B$ et $C$ sont trois points alignés $A’, B’$ et $C’$. On dit que la symétrie axiale conserve l’alignement.

Exemple :

IV- Symétrique d’un angle :

Propriété 6 :

Le symétrique d’un angle par une symétrie axiale est un angle de même mesure.

Exemple :

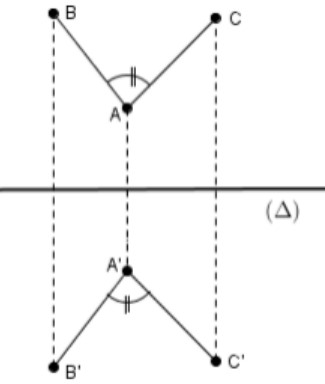
On a : $A’, B’$ et$ C’$ sont les symétriques respectifs des points $A, B$ et $C$ par rapport à la droite $(∆)$.

Donc : le symétrique d’angle $\widehat{ABC}$ par rapport à la droite $(∆)$ est l’angle $\widehat{A’B’C’}$ , de plus : $\widehat{ABC}=\widehat{A’B’C’}$

Propriété 7 :

La symétrie centrale conserve les mesures des angles.

V- Symétrique d’un cercle :

Propriété 8 :

Le symétrique d’un cercle par une symétrie axiale est un cercle de même rayon $r$.

Exemple :

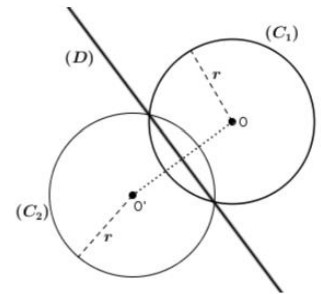
Le symétrique d’un cercle $\boldsymbol{C 1}(\mathrm{O} ; \mathrm{r})$ par rapport à la droite $(\mathrm{D})$ est un cercle $\boldsymbol{C 2}\left(\mathrm{O}^{\prime} ; \mathrm{r}\right)$ tel que $\mathrm{O}^{\prime}$ est le symétrique de O par rapport à (D).