Symétrie axiale – Évaluations corrigés

Modèle $N°1$

Exercice 1: $(4 pts)$

$1)$ Tracer un triangle $ABC$ comme ci-dessous :

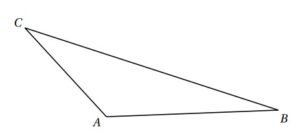
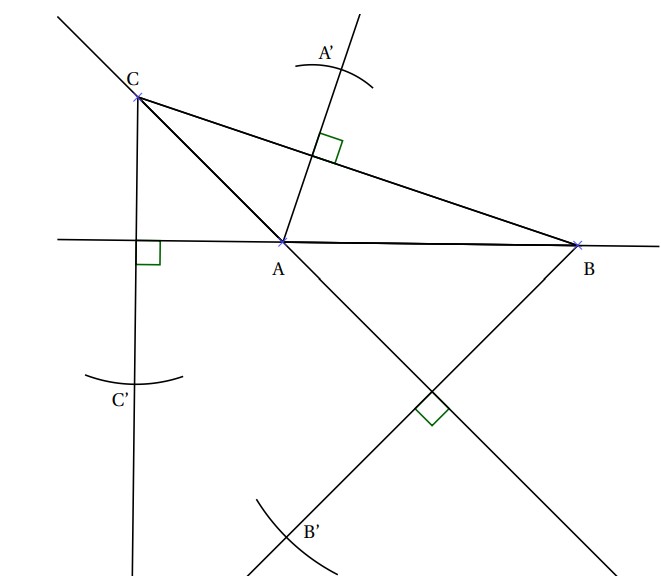
$2)$ Construire les points :

• $A′$ symétrique de $A$ par rapport à la droite $(BC)$;

• $B′$ symétrique de $B$ par rapport à la droite $(AC)$;

• $C′$ symétrique de $C$ par rapport à la droite $(AB)$;

Exercice 2 : $(6 pts)$

Adam doit construire une figure. Voici les différentes instructions, dans le désordre. Les remettre dans un ordre correct et construire la figure de Adam.

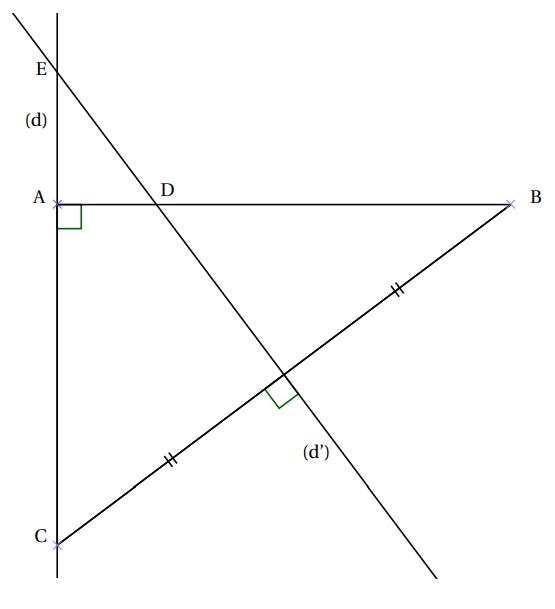
$1)$ Tracer un segment $[AB]$ de longueur $8 cm$.

$2)$ Tracer la perpendiculaire $(d)$ en A à la droite $(AB)$.

$3)$ Placer un point $C$ de la droite $(d)$ tel que $AC = 6 cm$.

$4)$ Tracer le segment $[BC]$.

$5)$ Tracer la médiatrice $(d’)$ du segment $[BC]$.

Exercice 3 : $(2 pts)$

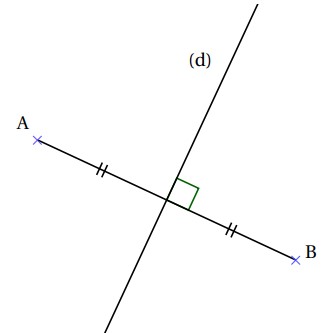
$1)$ Placer deux points $A$ et $B$ distincts.

$2)$ Inass propose un défi : » Si je te dis que $A$ et $B$ sont symétriques par rapport à une droite $(d)$.

Es-tu capable de tracer la droite $(d)$ avec les instruments de géométrie ? »

Exercice 4 : $(8 pts)$

Les triangles ci-dessous sont symétriques par rapport à la droite $(d)$.

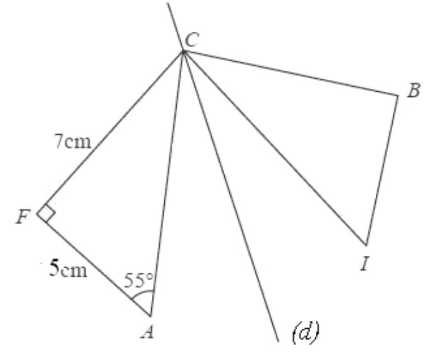
$1)$ Quel autre angle de la figure a pour mesure $55^{\circ}$ ? Justifier la réponse.

$2)$ Quelle est la longueur du segment $[B I]$ ? Justifier la réponse.

$3)$ Quelle est la nature du triangle $B I C$ ? Justifier la réponse.

$4)$ Calculer l’aire du triangle $B I C$.