Théorème de Thalès – Cours

I- Le théorème de Thales direct

1. Enoncé du théorème

Théorème :

$(D)$ et $(\Delta)$ deux droites sécantes en $A$

Soient $B$ et $M$ deux points de la droite $(D)$ distinctes de $A$

Soient $C$ et $N$ deux points de la droite $(\Delta)$ distinctes de $A$

Si $(B C) \|(M N)$ alors : $\quad \frac{A M}{A B}=\frac{A N}{A C}=\frac{M N}{B C}$

Trois configurations illustrent ce théorème

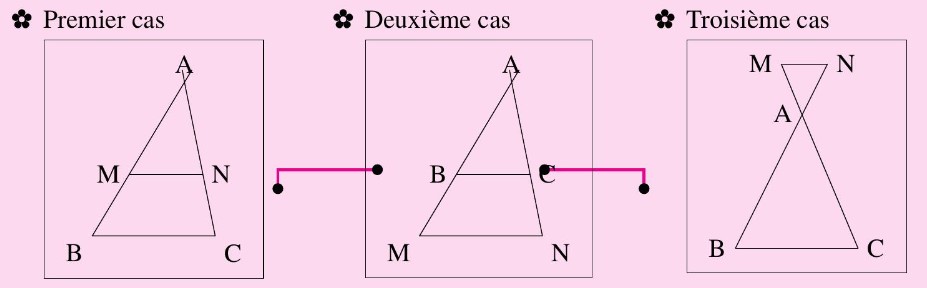
2. Application sur le triangle

Proposition

Soit $A B C$ un triangle

Si $\left\{\begin{array}{l}M \in[A B] \\ N \in(A C]\end{array}\right.$ tel que $(M N) \|(B C)$

Alors $\frac{A M}{A B}=\frac{A N}{A C}=\frac{M N}{B C}$

Remarque

• Le théorème de Thalès direct nécessite deux conditions, a savoir, l’appartenance et le parallélisme et donne la triple égalité .

• On utilise le théorème de Thalès direct pour calculer les longueurs.

Exemple :

Soit $A B C$ un triangle tel que : $A B=6 \mathrm{~cm}, A C=4 \mathrm{~cm}$ et $B C=5 \mathrm{~cm}$

Soit $E$ un point de $[A B]$ tel que $A E=2 \mathrm{~cm}$

la parallèle à $(B C)$ passante par $E$ coupe $[A C]$ en $F$

1) Construire une figure

2) Calculer $A F$ et $A E$

Solution

1) Construisons une figure

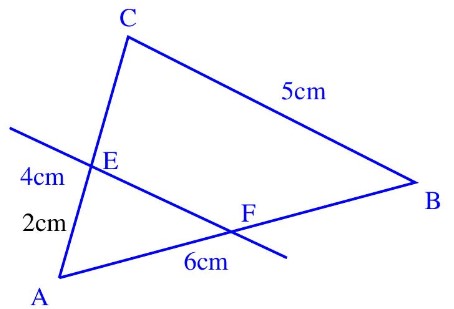
2) Calculons $A F$ et $A E$ On considère le triangle $A B C$

On a : $\left\{\begin{array}{l}E \in[A B] \\ F \in(A C]\end{array}\right.$ tel que $(E F) \|(B C)$

Donc d’après le théorème de Thalès direct, on a : $\frac{A E}{A B}=\frac{A F}{A C}=\frac{E F}{B C}$

C’est à dire : $\frac{2}{6}=\frac{A F}{4}=\frac{E F}{5}$, Donc : $\frac{2}{6}=\frac{A F}{4}$ et $\frac{2}{6}=\frac{E F}{5}$

Donc : $A F=\frac{2 \times 4}{6}$ et $E F=\frac{2 \times 5}{6}$, D’où $: A F=\frac{4}{3} c m$ et $E F=\frac{5}{3} c m$

II. La réciproque du théorème de Thalès

1. Théorème de Thalès réciproque

Théorème: 

Soient $(D)$ et $(\Delta)$ deux droites sécantes en $A$

$B$ et $M$ deux points de (D) disticts de $A$

$C$ et $N$ deux point de ( $\Delta$ ) distincts de $A$

Si les points $A, M$ et $B$ et les points $A, N$ et $C$ ont le même ordre tel que $\frac{A M}{A B}=\frac{A N}{A C}$

Alors : $(M N) \|(B C)$

2.  Application sur le triangle

Proposition

Soit $A B C$ un triangle

$\mathrm{Si}\left\{\begin{array}{l}\star M \in[A B] \\ \star N \in[A C]\end{array}\right.$

et les points $A, M$ et $B$ et les points $A, N$ et $C$ ont le même ordre tel que $\frac{A M}{A B}=\frac{A N}{A C}$ Alors : $(M N) \|(B C)$

Remarque

• Le théorème de Thalès réciproque nécessite trois conditions ( Appartenance + Ordre des points + Egalité ) et donne le parallélisme.

• On utilise la réciproque du théorème de Thalès pour prouver le parallélisme.

• La condition de l’ordre des points sur chaque droite est nécessaire pour applique la réciproque du théorème de Thalès.

 Exemple:

On considère la figure suivantes

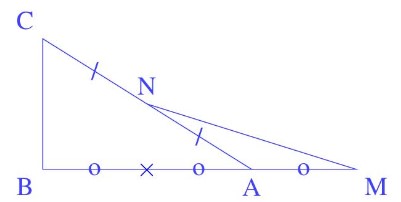
On a : $\frac{A M}{A B}=\frac{1}{2}$ et $\frac{A N}{A C}=\frac{1}{2}$

Donc : $\frac{A M}{A B}=\frac{A N}{A C}$

Et pourtant $(M N)$ et $(B C)$ ne sont pas parallèles, car l’ordre des points $A, N$ et $C$ est différent de l’ordre des points $A, M$ et $B$

Application

Soit $A B C$ un triangle tel que : $A B=4 \mathrm{~cm}$ et $A C=6 \mathrm{~cm}$

$E$ est un point de $[A B]$ tel que $A E=2 \mathrm{~cm}$ et $F$ est un point de $[A C]$ tel que $A F=3 \mathrm{~cm}$

1) Construire une figure

2) Montrer que : $(B C) \|(E F)$

Solution

1) Construisons une figure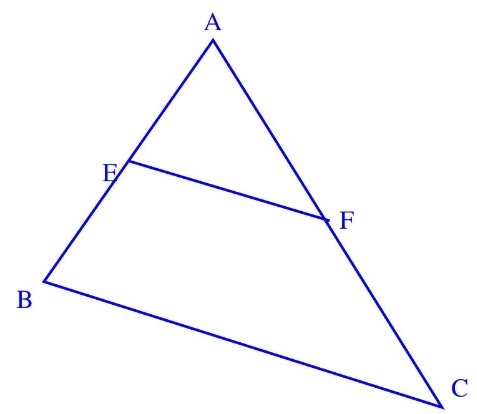

2) Montrons que : $(B C) \|(E F)$

On a $\frac{A E}{A B}=\frac{2}{4}=\frac{1}{2}$ et $\frac{A F}{A C}=\frac{3}{6}=\frac{1}{2}$

Donc : $\frac{A E}{A B}=\frac{A F}{A C}$

On considère le triangle $A B C$

On a : $\left\{\begin{array}{l}E \in(A B) \\ F \in(A C)\end{array}\right.$

Et les points $A, E$ et $B$ et les points $A, F$ et $C$ ont le même ordre et puisque $\frac{A E}{A B}=\frac{A F}{A C}$

Donc, d’après le théorème de Thalès réciproque, on a : $(B C) \|(E F)$