Théorème de Thalès – Évaluations corrigés
Modèle $N°1$
Exercice 1：$(6pts)$
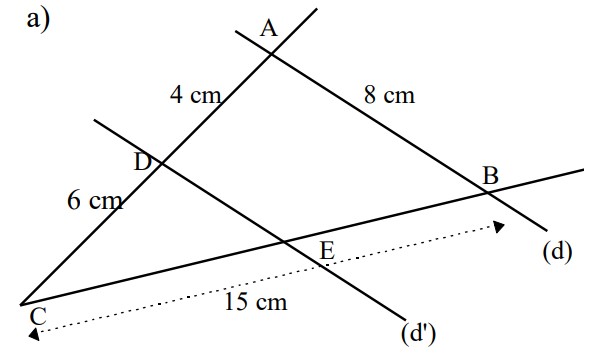
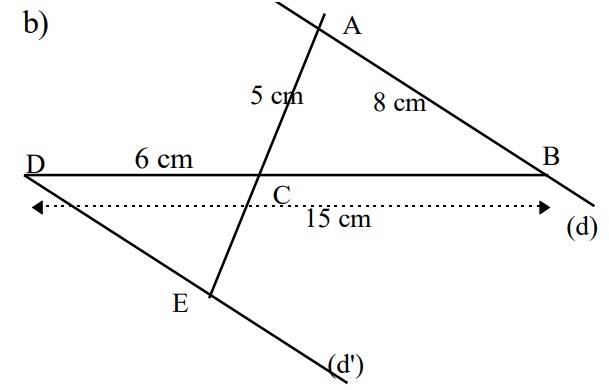
Sachant que l’on a $(d) // (d’)$, calculer $CE$ et $DE$ dans les 2 cas ci-dessous. Justifier.
Exercice 2：$(3pts)$
On donne : $\mathrm{AB}=30$ ; $\mathrm{AD}=75 $ ; $\mathrm{AC}=20$ ; $\mathrm{AE}=50 $ ; $\mathrm{AF}=12 $
$1)$ Tracer les segments $[EB]$ et $[CF]$.
$2)$ Les droites $(EB)$ et $(CF)$ sont-elles parallèles ?
Exercice 3：$(3pts)$
La figure ci-contre n’est pas en vraie grandeur.
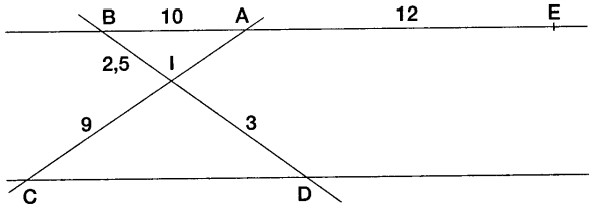
Les droites $(AB)$ et $(CD)$ sont parallèles.
Les dimensions de la figure sont les suivantes :
$ \mathrm{IB}=2,5$ ; $\mathrm{AB}=10$ ; $\mathrm{ID}=3 $ $ \mathrm{AE}=12$ ; $\mathrm{IC}=9$
• Les droites $(AI)$ et $(DE)$ sont-elles parallèles ? Justifier.
Exercice 4：$(3pts)$
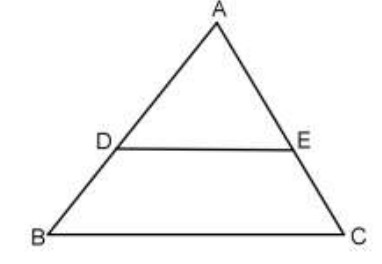
Les droites $(DE)$ et $(BC)$ sont parallèles.
• Calculer $AD$ sachant que $BD = 3$ , $DE = 7$ et $BC = 20$
Exercice 5：$(5pts)$
Des bateaux participent à une régate. Ils doivent suivre le parcours suivant (en gras et fléché sur la figure):
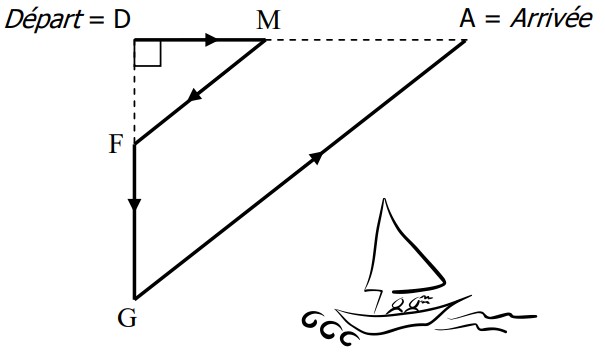
On donne :
$\mathrm{DM}=8 \mathrm{~km}, \mathrm{DF}=6 \mathrm{~km}$
$\mathrm{MA}=2 \times \mathrm{DM}, \mathrm{FDM}=90^{\circ}$
$F \in(D G) ~et~ M \in(D A)$
Les droites $(FM)$ et $(AG)$ sont parallèles.
$1)$ Calculer $FM$.
$2)$ Calculer $FG$.
$3)$ Calculer $AG$.
$4)$ Vérifier que la longueur de la régate est de $60 km$.
Théorème de Thalès – Évaluations corrigés
$a)$ Les droites $(AD)$ et $ (BE) $ se coupent en $C$ et $(AB) // (CE)$. D’après le théorème de Thalès :
$\frac{C D}{C A}=\frac{C E}{C B}=\frac{D E}{A B} \text { soit : } \frac{6}{10}=\frac{C E}{15}=\frac{D E}{8}$
$\frac{6}{10}=\frac{\mathrm{CE}}{15} ~soit : 10 \times \mathrm{CE}=6 \times 15 ~~et~~ \mathrm{CE}=\frac{6 \times 15}{10}=9 \mathrm{~cm}$
$\frac{6}{10}=\frac{\mathrm{DE}}{8}~ soit : 10 \times \mathrm{DE}=6 \times 8~~ et ~~\mathrm{DE}=\frac{6 \times 8}{10}=4,8 \mathrm{~cm}$
$b)$ Les droites $(AE)$ et $(BD)$ se coupent en $C$ et $(AB) // (DE)$. D’après le théorème de Thalès :
$\frac{C D}{C B}=\frac{C E}{C A}=\frac{D E}{B A} \text { soit }: \frac{6}{9}=\frac{C E}{5}=\frac{D E}{8}$
$\frac{6}{9}=\frac{\mathrm{CE}}{5}~ soit : 9 \times \mathrm{CE}=6 \times 5~~ et ~~\mathrm{CE}=\frac{6 \times 5}{9}=\frac{10}{3} \mathrm{~cm}$
$\frac{6}{9}=\frac{\mathrm{DE}}{8}~ soit : 9 \times \mathrm{DE}=6 \times 8~~ et ~~\mathrm{DE}=\frac{6 \times 8}{9}=\frac{16}{3} \mathrm{~cm}$
$\frac{\mathrm{AC}}{\mathrm{AE}}=\frac{20}{50}=\frac{2}{5}~~ et ~~\frac{\mathrm{AF}}{\mathrm{AB}}=\frac{12}{30}=\frac{2 \times \frac{6}{6}}{5 \times \frac{6}{6}}=\frac{2}{5}$
Ainsi : $\frac{A F}{A B}=\frac{A C}{A E} $ et les points $A, C, E$ et les points $A, F, B$ sont alignés dans le même ordre.
D’après la réciproque du théorème de Thalès, les droites $(EB)$ et $(CF)$ sont parallèles.
$\frac{\mathrm{BA}}{\mathrm{BE}}=\frac{10}{22}=\frac{5}{11}~~ et ~~\frac{\mathrm{BI}}{\mathrm{BD}}=\frac{2,5}{5,5}=\frac{2 \times 2,5}{2 \times 5,5}=\frac{5}{11}$
Ainsi : $\frac{B A}{B E}=\frac{B I}{B D}$ et les points $B, A, E$ et les points $B, I, D$ sont alignés dans le même ordre.
D’après la réciproque du th. de Thalès, $(AI)$ et $(DE)$ sont parallèles.
$\quad \mathrm{BD}=3, \mathrm{DE}=7~~ et ~~\mathrm{BC}=20 ; \mathbf{A D}=\mathbf{x}$
Les droites $(BD)$ et $(CE)$ se coupent en $A$ et $(BC) // (DE)$
D’après le théorème de Thalès : $\frac{A D}{A B}=\frac{A E}{A C}=\frac{D E}{B C}$
Soit : $\frac{x}{x+3}=\frac{A E}{A C}=\frac{7}{20}$
$\frac{x}{x+3}=\frac{7}{20}$
$x \times 20=7 \times(x+3) $
$ 20 x=7 x+21 $
$ 13 x=21 $
$ x= AD = \frac{21}{13}$
$1)$ Le triangle $DFM$ est rectangle en $D$. Théorème de Pythagore :
$\mathrm{FM}^{2}=\mathrm{DF}^{2}+\mathrm{DM}^{2}=6^{2}+8^{2}=100 \text { donc } \mathrm{FM}=\sqrt{100}=10 \mathrm{~km}$
$2)$ Les droites $(FG)$ et $(AM)$ se coupent en $D$ et $( FM ) // (AG)$.
D’après le théorème de Thalès : $\frac{\mathrm{DM}}{\mathrm{DA}}=\frac{\mathrm{DF}}{\mathrm{DG}}=\frac{\mathrm{MF}}{\mathrm{AG}} $
Soit : $\frac{8}{24}=\frac{6}{\mathrm{DG}}=\frac{10}{\mathrm{AG}} $
$\mathrm{DM}= \mathrm{DF}+ \mathrm{MA}=\mathrm{DF}+ 2 \times \mathrm{DM}=3 \times \mathrm{DM}=3 \times \mathrm{8}=24 \mathrm{~km}$
$ \mathrm{DG}=\frac{24 \times 6}{8}=18 \mathrm{~km}$
Donc : $\mathrm{FG}= \mathrm{DG}- \mathrm{DF}=18 -6=12\mathrm{~km}$
$3)$ Calculer $AG$
$On~ a :\frac{8}{24}=\frac{6}{\mathrm{DG}}=\frac{10}{\mathrm{AG}} $
$ \mathrm{AG}=\frac{24 \times 10}{8}=30 \mathrm{~km}$
$4)$ Vérifier que la longueur de la régate est de $60 km$.
$\mathrm{DM}+ \mathrm{FM}+ \mathrm{FG}+ \mathrm{AG}=8+10+12+30 =60\mathrm{~km}$
Théorème de Thalès – Évaluations corrigés